Question

Sum of the series $\frac{1}{2}+\frac{1+2}{3}+\frac{1+2+3}{4}+...20$ terms is equal to

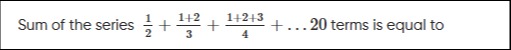
Answer 1

105

Answer 2

The $n$-th term of the series is $T_n = \frac{1+2+...+n}{n+1} = \frac{n(n+1)/2}{n+1} = \frac{n}{2}$. The sum of 20 terms is $S_{20} = \sum_{n=1}^{20} \frac{n}{2} = \frac{1}{2} \sum_{n=1}^{20} n$. Using the formula $\sum_{n=1}^{N} n = \frac{N(N+1)}{2}$, we get $S_{20} = \frac{1}{2} \times \frac{20(20+1)}{2} = \frac{1}{2} \times 210 = 105$.