Question

From a point R on major axis of ellipse $\frac{x^2}{16}+\frac{y^2}{9}=1$ two perpendicular normal are drawn intersecting ellipse at P & Q and area of $\triangle PQR$ is $\lambda$, then value of $25\lambda$ is

Answer 1

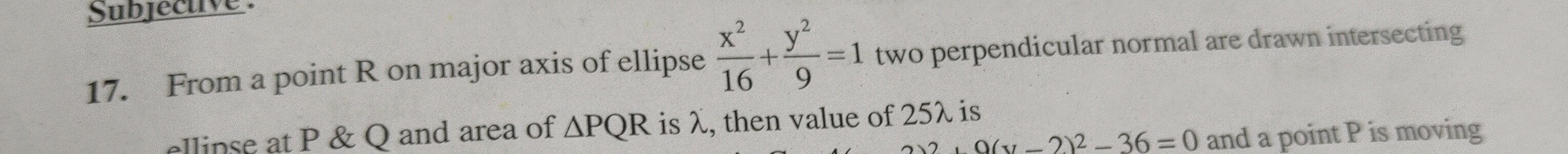
144

Answer 2

The ellipse is $\frac{x^2}{16}+\frac{y^2}{9}=1$, so $a^2=16$ and $b^2=9$. R is on the major axis, so R is $(h, 0)$. For two perpendicular normals to be drawn from R to the ellipse, R must lie on the director circle $x^2+y^2 = a^2+b^2$. Thus, $h^2+0^2 = 16+9=25$, which means $h=\pm 5$. Let R be $(5,0)$. The slopes of the normals from $(h,0)$ are given by $m^2 = \frac{b^2}{a^2-h^2}$ when $b^2=a^2$ (which is not the case here) or from $m^2(h^2-a^2) - b^2 = 0$. With $h^2=25$, $a^2=16$, $b^2=9$, we get $m^2(25-16) - 9 = 0 \implies 9m^2 = 9 \implies m^2=1$. So the slopes are $m=1$ and $m=-1$. The slope of the normal at $(a \cos \theta, b \sin \theta)$ is $m = -\frac{b}{a} \cot \theta$. For $m=1$, $1 = -\frac{3}{4} \cot \theta_1 \implies \cot \theta_1 = -4/3$. For $m=-1$, $-1 = -\frac{3}{4} \cot \theta_2 \implies \cot \theta_2 = 4/3$. If $\cot \theta_1 = -4/3$, we can take $\cos \theta_1 = -4/5, \sin \theta_1 = 3/5$. If $\cot \theta_2 = 4/3$, we can take $\cos \theta_2 = 4/5, \sin \theta_2 = 3/5$. Thus, $P = (4(-4/5), 3(3/5)) = (-16/5, 9/5)$ and $Q = (4(4/5), 3(3/5)) = (16/5, 9/5)$. The base PQ has length $\frac{16}{5} - (-\frac{16}{5}) = \frac{32}{5}$. The height of $\triangle PQR$ from R $(5,0)$ to the line $y=9/5$ is $9/5$. The area $\lambda = \frac{1}{2} \times \frac{32}{5} \times \frac{9}{5} = \frac{144}{25}$. Therefore, $25\lambda = 25 \times \frac{144}{25} = 144$.