Question

such that $ABCD_{10}=4x$.

Cube A is circumscribed by a sphere of radius 3, while a congruent sphere is inscribed inside Cube B. What is the ratio of the volume of Cube B to the volume of Cube A? Express your answer in simple radical form.

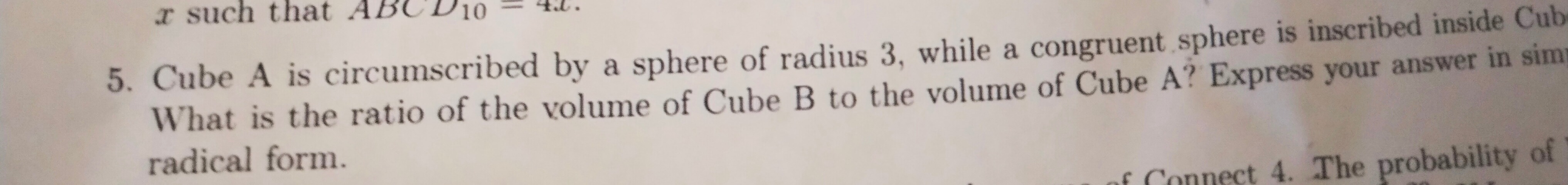
Answer 1

3\sqrt{3}

Answer 2

Let the side of Cube A be $s_A$. For a cube circumscribed by a sphere (i.e., the sphere passes through all vertices), the relationship between the side $s$ and the radius $R$ of the sphere is:

$$R = \frac{s\sqrt{3}}{2}$$

For Cube A, $R = 3$:

$$3 = \frac{s_A\sqrt{3}}{2} \quad \Longrightarrow \quad s_A = \frac{6}{\sqrt{3}} = 2\sqrt{3}.$$

For Cube B, a sphere of radius 3 is inscribed in it. In this case, the diameter of the sphere equals the side of the cube:

$$s_B = 2 \times 3 = 6.$$

Volume of Cube A:

$$V_A = s_A^3 = (2\sqrt{3})^3 = 8 \times 3\sqrt{3} = 24\sqrt{3}.$$

Volume of Cube B:

$$V_B = s_B^3 = 6^3 = 216.$$

The ratio of the volumes is:

$$\frac{V_B}{V_A} = \frac{216}{24\sqrt{3}} = \frac{9}{\sqrt{3}} = \frac{9\sqrt{3}}{3} = 3\sqrt{3}.$$