Question

In the arrangement shown, initially spring is in natural length and the system is released, range of normal reaction on the block of mass 5 kg is (Spring, string and pulley are ideal)

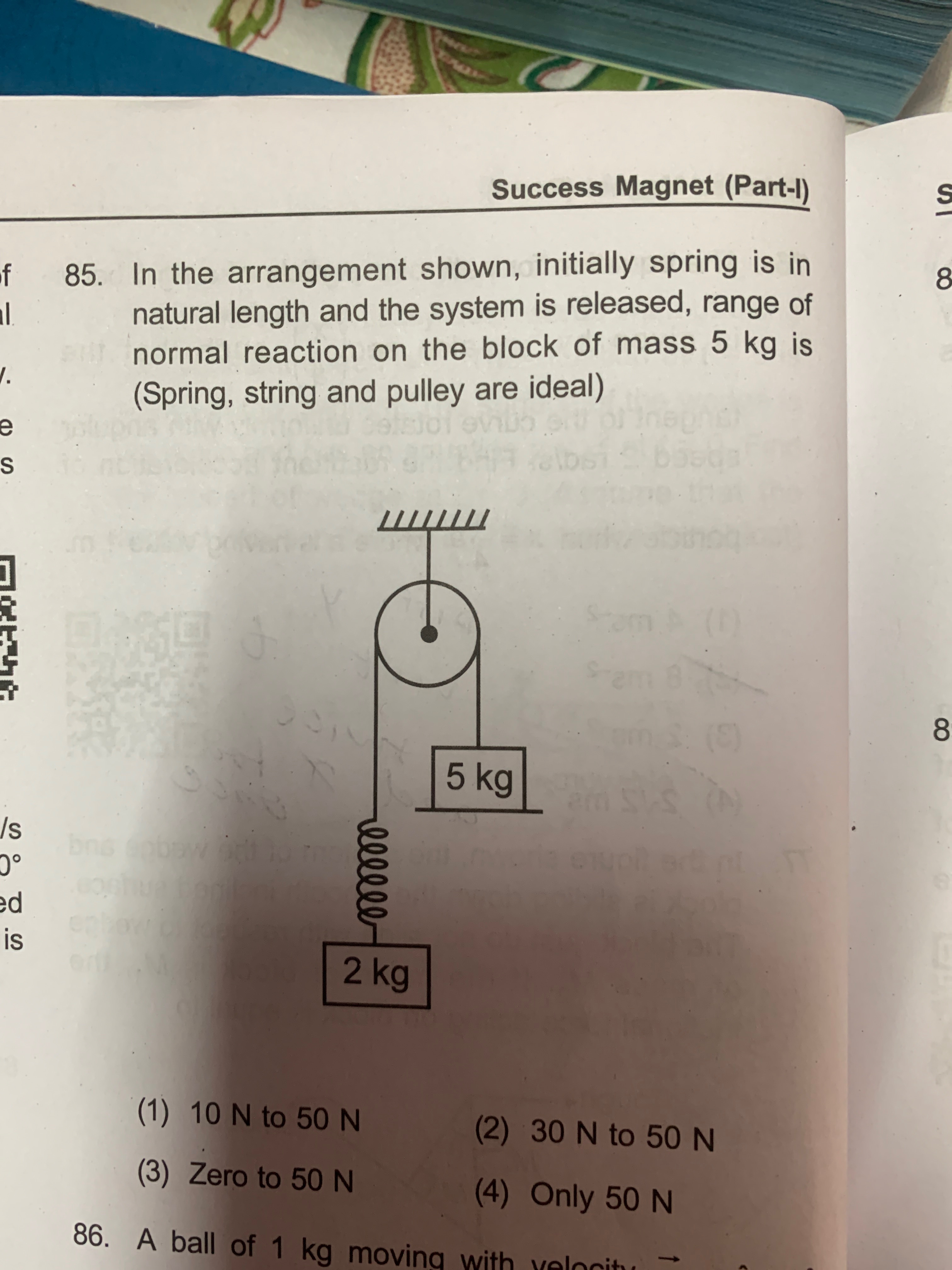
• A. 10 N to 50 N
• B. 30 N to 50 N
• C. Zero to 50 N
• D. Only 50 N

Answer 1

Answer: (B)

30 N to 50 N

Answer 2

We note that the 5‐kg block rests on a horizontal (ideal) surface and is connected by a light string that runs over an ideal pulley. One end of the string is attached to the 5‐kg block and the other end goes to a spring (initially unstretched) in series with a 2‐kg mass. Since the pulley is fixed (at the edge of the table) and the string is inextensible, the string joining the 5‑kg block to the pulley is not necessarily horizontal; rather it makes an angle θ with the horizontal. Thus the block suffers a tension force T whose vertical component is T sinθ.

For the block on the table, the vertical forces are:

Normal reaction $N$ (upward)

Weight $(5g=50\,\text{N},\ \text{downward})$

Vertical component of tension: $T\sin\theta$ (upward)

Since there is no vertical motion,

$$N + T\sin\theta = 50\quad \Longrightarrow \quad N = 50 - T\sin\theta.$$

Key points:

1. Initial stage: When the system is released, the spring is at its natural length so no force is transmitted through it, meaning $T=0$. Then $N=50\,\text{N}$.

2. Later motion: As the 2‐kg mass falls, the spring stretches and develops a tension $T$ that increases gradually. Simultaneously the 5‐kg block moves toward the pulley. In the limit when the block is very close to the pulley the string becomes almost vertical, i.e. $\sin\theta\to 1.$

At this stage the vertical upward force on the block becomes maximum: $T\sin\theta \approx T$. The maximum value of $T$ (which can be determined from the dynamics of the 2‐kg–spring system) turns out to be such that the maximum vertical pull on the 5‑kg block is about 20 N (since the 2‐kg weight, when decelerated by the spring, can at most “pull” with a force of the order of its weight). Therefore the minimum normal reaction becomes

$$N_{\min}=50-20=30\,\text{N}.$$

Thus the normal reaction on the 5‑kg block will vary between 30 N and 50 N.