Question
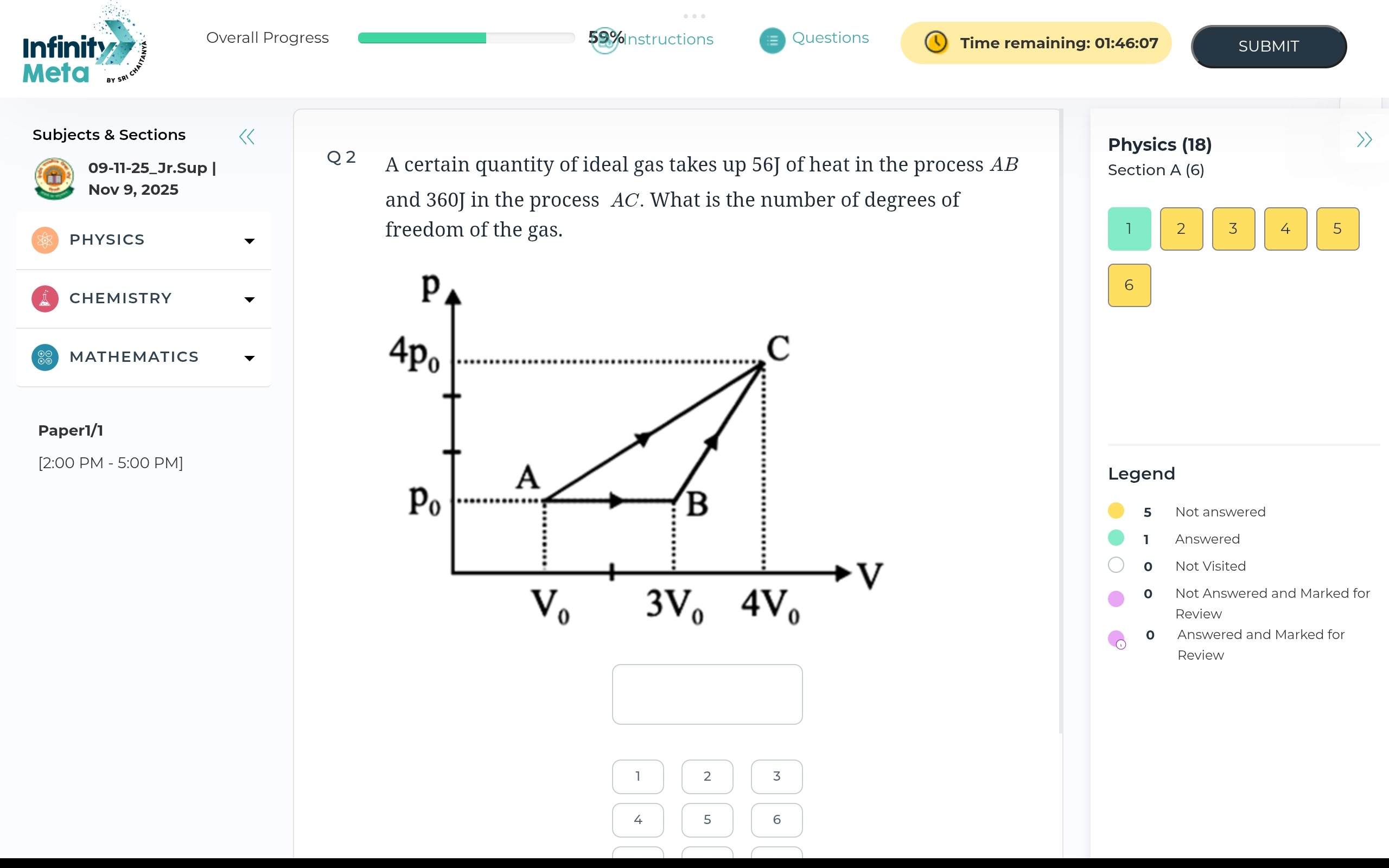
Question: A certain quantity of ideal gas takes up 56J of heat in the process $AB$ and 360J in the process $AC...
A certain quantity of ideal gas takes up 56J of heat in the process AB and 360J in the process AC. What is the number of degrees of freedom of the gas.
Answer
5
Explanation
Solution
For process AB (isobaric): QAB=56 J WAB=p0(3V0−V0)=2p0V0 ΔUAB=2f(p0(3V0)−p0V0)=fp0V0 Using the First Law of Thermodynamics (Q=ΔU+W): 56=fp0V0+2p0V0=(f+2)p0V0 (1)
For process AC (linear, P∝V): QAC=360 J WAC=∫V04V0V0p0VdV=215p0V0 ΔUAC=2f(4p0(4V0)−p0V0)=215fp0V0 Using the First Law of Thermodynamics: 360=215fp0V0+215p0V0=215(f+1)p0V0 (2)
Dividing (2) by (1): 56360=(f+2)p0V0215(f+1)p0V0 745=215f+2f+1 76=f+2f+1 6(f+2)=7(f+1) 6f+12=7f+7 f=5
