Question

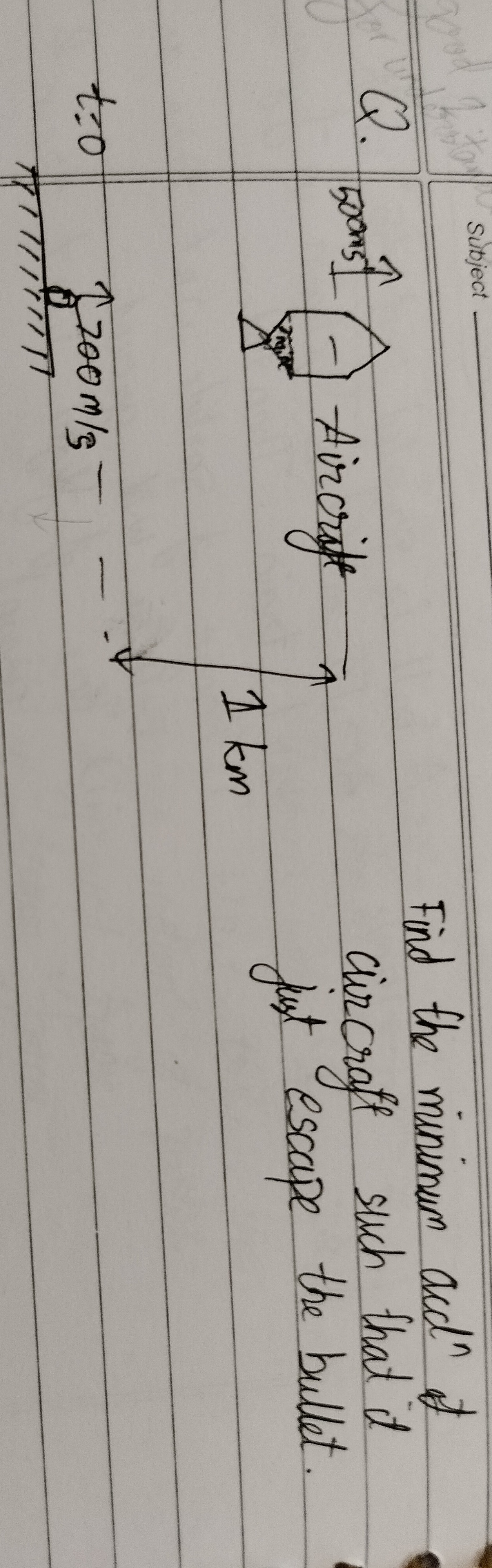
Aircrift

Find the minimum acd ot circraft such that it just escape the bullet.

1 km

1:0

$200m/5-$

Answer 1

10

Answer 2

The aircraft is initially at a height $h = 1$ km = 1000 m above the ground. The bullet is fired vertically upwards from the ground with an initial velocity $v_b = 200$ m/s. The aircraft starts accelerating upwards with a constant acceleration $a$. We assume the initial vertical velocity of the aircraft is 0. Let the vertical position of the ground be $y=0$. The vertical position of the bullet at time $t$ is given by $y_b(t) = v_b t - \frac{1}{2} g t^2$. The vertical position of the aircraft at time $t$ is given by $y_a(t) = h + \frac{1}{2} a t^2$.

A collision occurs if $y_b(t) = y_a(t)$ for some time $t > 0$. $v_b t - \frac{1}{2} g t^2 = h + \frac{1}{2} a t^2$ Rearranging the terms, we get a quadratic equation in $t$: $\frac{1}{2}(g+a)t^2 - v_b t + h = 0$

For the aircraft to just escape the bullet, the bullet should not hit the aircraft. This means the quadratic equation should have no real roots for $t>0$, or exactly one real root (which corresponds to the bullet just touching the aircraft). The discriminant of the quadratic equation $At^2 + Bt + C = 0$ is $D = B^2 - 4AC$. In our equation, $A = \frac{1}{2}(g+a)$, $B = -v_b$, and $C = h$. The discriminant is $D = (-v_b)^2 - 4 \left(\frac{1}{2}(g+a)\right) h = v_b^2 - 2h(g+a)$.

For the aircraft to escape, we need the quadratic equation to have no real roots or exactly one real root. This happens when the discriminant $D \le 0$. $v_b^2 - 2h(g+a) \le 0$ $v_b^2 \le 2h(g+a)$ Since $h > 0$ and $g+a > 0$ (assuming $a \ge 0$, and $g>0$), we can divide by $2h$: $\frac{v_b^2}{2h} \le g+a$ $a \ge \frac{v_b^2}{2h} - g$

The minimum acceleration required for the aircraft to escape is when the equality holds, i.e., $D=0$. $a_{min} = \frac{v_b^2}{2h} - g$.

We are given $v_b = 200$ m/s and $h = 1000$ m. We need to use a value for $g$. Let's assume $g = 10$ m/s$^2$. $a_{min} = \frac{(200)^2}{2 \cdot 1000} - 10 = \frac{40000}{2000} - 10 = 20 - 10 = 10$ m/s$^2$.

If we use $g = 9.8$ m/s$^2$: $a_{min} = \frac{(200)^2}{2 \cdot 1000} - 9.8 = 20 - 9.8 = 10.2$ m/s$^2$.

Without a specified value for $g$, both 10 m/s$^2$ and 9.8 m/s$^2$ are common. If the options are integers, 10 m/s$^2$ is likely the intended answer. If the options are decimal values, 10.2 m/s$^2$ might be the answer. Since no options are provided, we will provide the answer assuming $g=10$ m/s$^2$.

The minimum acceleration of the aircraft such that it just escape the bullet is 10 m/s$^2$.