Question
Question: $\left(2+\sqrt{5}\right)^{\frac{1}{3}}+\left(2-\sqrt{5}\right)^{\frac{1}{3}}$...
(2+5)31+(2−5)31
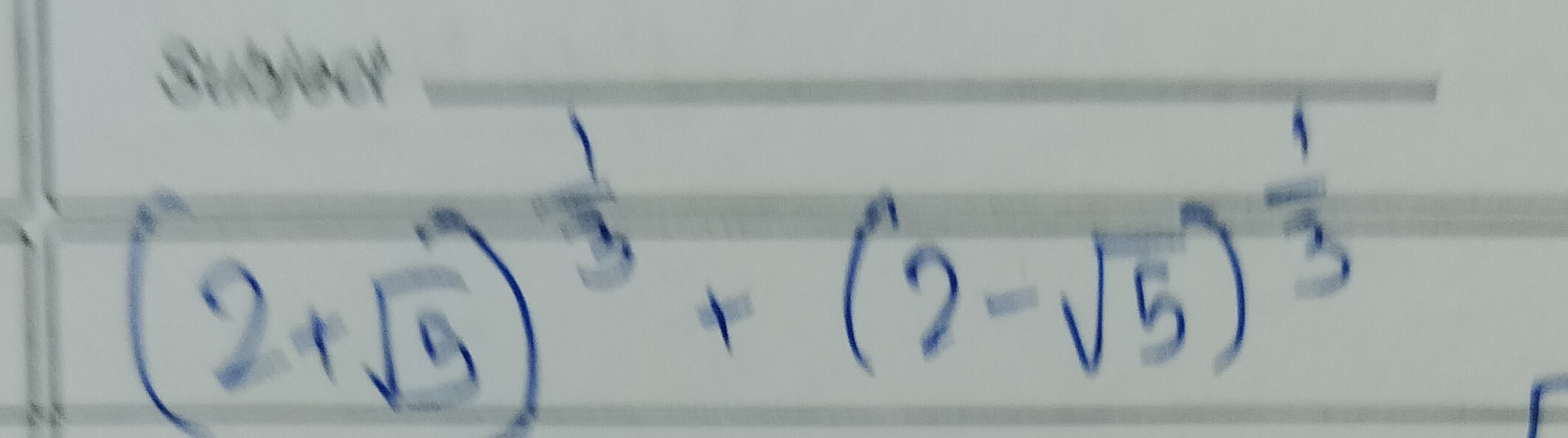
1
Solution
Let x=(2+5)31+(2−5)31. Cube both sides using the formula (a+b)3=a3+b3+3ab(a+b). Let a=(2+5)31 and b=(2−5)31. Then x3=a3+b3+3ab(a+b).
a3=((2+5)31)3=2+5 b3=((2−5)31)3=2−5 ab=(2+5)31(2−5)31=((2+5)(2−5))31=(4−5)31=(−1)31=−1
Substituting these values into the cubed equation: x3=(2+5)+(2−5)+3(−1)(x) x3=4−3x Rearrange the equation to form a cubic equation: x3+3x−4=0
We need to find the real root(s) of this equation. We can test integer divisors of the constant term (-4), which are ±1,±2,±4. Let's test x=1: 13+3(1)−4=1+3−4=0. So, x=1 is a root.
We can factor the cubic polynomial using the root x=1. (x−1) is a factor. Using polynomial division or synthetic division: (x3+3x−4)÷(x−1)=x2+x+4. So, the equation is (x−1)(x2+x+4)=0. The roots are x=1 or x2+x+4=0. Consider the quadratic equation x2+x+4=0. The discriminant is Δ=b2−4ac=12−4(1)(4)=1−16=−15. Since the discriminant is negative, the quadratic equation has two complex conjugate roots. The roots are x=2−1±−15=2−1±i15. The only real root of x3+3x−4=0 is x=1.
Since the expression (2+5)31+(2−5)31 must be a real number, its value is the real root of the cubic equation, which is 1.
