Question
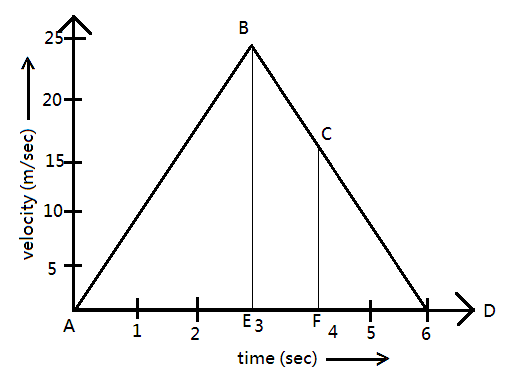
Question: Study the velocity-time graph and calculate. A. The acceleration from A to B B. The acceleration...
Study the velocity-time graph and calculate.
A. The acceleration from A to B
B. The acceleration from B to C
C. The distance covered in the region ABE
D. The average velocity from C to D
E. The distance covered in the region BCFE
Solution
There are five sub parts of this question, read each sub-part carefully and then solve the problem. The slope of the velocity time graph is acceleration. To find the distance covered using a kinematical equation, we have velocity, time and acceleration to distance travelled can be easily calculated.
Complete step by step answer:
The given diagram depicts a motion in which a particle starts from point A at time t=0 and then it accelerates till it reaches point B. From point B the particle decelerates till t=6s . On the X-axis we have time and, on the Y-axis, we have velocity.
As we have discussed in the hint section, acceleration is the slope of the velocity time graph.
Also, we have the kinematical equation, v−u=at
Here v is the final velocity, u is the initial velocity, t is the time taken and a is the acceleration.
From this equation, we can have
a=tv−u
From the graph we have the following values when the particle travels from A to B.
v=25ms−1 , u=0ms−1 and t=3s , substituting these values in the above equation, we have
a=325−0
⇒a=325=8.33ms−2
Therefore, the acceleration from A to B is 8.33ms−2 .
The acceleration from B to C.
From the graph we have the following values when the particle travels from B to C.
v=20ms−1 , u=25ms−1 and t=1s , substituting these values in the above equation, we have
a=120−25
⇒a=−5ms−2
The acceleration from B to C is −5ms−2 .
The negative sign implies that the body is decelerating.
Distance covered in region ABE.
Distance covered is given as the area under the velocity time graph.
Distance covered s will be given as
s=Area(△ABE)
⇒s=21×3×25
⇒s=37.5m
The distance travelled in the region ABE is 37.5m .
The average velocity from C to D.
The average velocity will be
vavg=220
vavg=10ms−1
The average velocity from C to D is 10ms−1 .
Distance covered in the region BCFE
Distance will be given as the area under BCFE region, the BCFE region comprises of triangle with height 5m , base EF=1m and a rectangle have having length CF=20m and breadth EF=1m
The distance covered s will be equal to the total area, it will be given as
s=21×1×5+20×1
⇒s=22.5m
The distance covered in the region BCFE is 22.5m .
Thus, a) the acceleration from A to B is 8.33ms−2
b) acceleration from B to C is −5ms−2 .
c) The distance travelled in the region ABE is 37.5m .
d) The average velocity from C to D is 10ms−1 .
e) The distance covered in the region BCFE is 22.5m.
Note:
The area under the velocity-time graph gives the distance travelled.
The slope of the velocity-time graph gives the magnitude as well as the direction of the acceleration.
If the slope of the velocity-time graph is positive, the body is accelerating else the body is not accelerating.
