Question
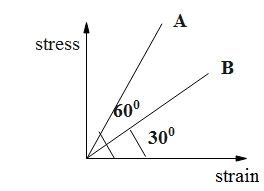
Question: Stress-strain curves for wire A & B are shown in figure then the product of Young’s modulus of \[{{Y...
Stress-strain curves for wire A & B are shown in figure then the product of Young’s modulus of YA×YBis.
Explanation
Solution
The stress-strain curve for a material gives the slope equal to that of Young’s modulus of that material. And, the slope is the angle of tan function. So, we will find the tan of angles of the wires A and B and then, we will multiply both to find the product of Young’s modulus of YA×YB.
Formula used:
& Y=\dfrac{\text{stress}}{\text{strain}} \\\ & \dfrac{\text{stress}}{\text{strain}}=\tan \theta \\\ \end{aligned}$$ **Complete step-by-step answer:** The Young’s modulus of a material in terms of stress and strain is given as follows. $$Y=\dfrac{\text{stress}}{\text{strain}}$$….. (1) As the curve of any graph is represented by the trigonometric function, that is, tan function, so, we have, $$\dfrac{\text{stress}}{\text{strain}}=\tan \theta $$…… (2) Equate the equations (1) and (2) to obtain the value of the slope of the function in terms of Young’s modulus of wires. $$Y=\tan \theta $$ As we are given with the two wires, so, we have, For the wire A, $${{Y}_{A}}=\tan {{\theta }_{A}}$$ And, for the wire B, $${{Y}_{B}}=\tan {{\theta }_{B}}$$ Substitute the given values in the above equations to find the values of the Young’s modulus of wires. So, we get, The Young’s modulus of wire A as follows. $$\begin{aligned} & {{Y}_{A}}=\tan 60{}^\circ \\\ & \Rightarrow {{Y}_{A}}=\sqrt{3} \\\ \end{aligned}$$…… (3) The Young’s modulus of wire B is as follows. $$\begin{aligned} & {{Y}_{B}}=\tan 30{}^\circ \\\ & \Rightarrow {{Y}_{B}}=\dfrac{1}{\sqrt{3}} \\\ \end{aligned}$$…… (4) Multiply the equations (3) and (4) to obtain the product of the Young’s modulus of wires A and B. $$\begin{aligned} & {{Y}_{A}}\times {{Y}_{B}}=\sqrt{3}\times \dfrac{1}{\sqrt{3}} \\\ & \Rightarrow {{Y}_{A}}\times {{Y}_{B}}=1 \\\ \end{aligned}$$ Therefore, the product of Young’s modulus of $${{Y}_{A}}\times {{Y}_{B}}$$is 1. **Note:** This is a neither tricky nor simple question. The curves are drawn to make the question a bit complicated. We only need the value of the slope of the angle made by the stress-strain curve to solve this type of question.