Question

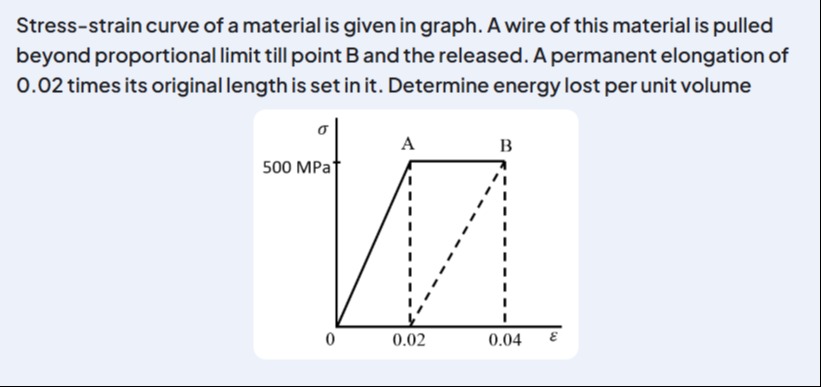
Stress-strain curve of a material is given in graph. A wire of this material is pulled beyond proportional limit till point B and the released. A permanent elongation of 0.02 times its original length is set in it. Determine energy lost per unit volume

Answer 1

Energy lost per unit volume = $5 \times 10^6$ J/m³.

Answer 2

Solution:

1. Determine the hysteresis area:

   • The loading path from A to B is a horizontal line at $\sigma = 500$ MPa from $\epsilon = 0.02$ to $\epsilon = 0.04$.
   • When released, the wire unloads along a straight line (elastic path) with the same slope as the initial elastic portion, intercepting the strain axis at $\epsilon = 0.02$.
   • The energy lost per unit volume is the area of the hysteresis loop. This area is the difference between the work done during loading (rectangle) and the work recovered during unloading (triangle).

2. Calculations:

   • Area of rectangle (loading between A and B): $$\text{Area}_\text{rect} = \sigma (\epsilon_B - \epsilon_A) = 500\,\text{MPa} \times (0.04-0.02) = 500\,\text{MPa} \times 0.02.$$
   • Area of triangle (during unloading): $$\text{Area}_\text{tri} = \tfrac{1}{2}\,\sigma (\epsilon_B - \epsilon_A) = \tfrac{1}{2}\,(500\,\text{MPa}\times0.02).$$
   • Energy lost per unit volume: $$E_\text{lost} = \text{Area}_\text{rect} - \text{Area}_\text{tri} = 500\,\text{MPa} \times 0.02 - \tfrac{1}{2}\,(500\,\text{MPa} \times 0.02).$$ $$E_\text{lost} = \tfrac{1}{2}\,(500\,\text{MPa} \times 0.02) = 0.5 \times (500 \times 10^6\,\text{Pa} \times 0.02).$$ $$E_\text{lost} = 0.5 \times (10 \times 10^6) \, \text{J/m}^3 = 5 \times 10^6\,\text{J/m}^3.$$

Explanation (minimal):

The energy lost per unit volume equals the hysteresis area between the loading (rectangle) and unloading (triangle) curves. Compute as

$$E_\text{lost} = \frac{1}{2}\sigma (\Delta\epsilon) = \frac{1}{2}(500\,\text{MPa})(0.02)=5\times10^6\,\text{J/m}^3.$$