Solveeit Logo
Login

Question

Question: Steel ruptures when a shear of \(3.5\times {{10}^{8}}N{{m}^{-2}}\) is applied. The force needed to p...

Steel ruptures when a shear of 3.5×108Nm−23.5\times {{10}^{8}}N{{m}^{-2}} is applied. The force needed to punch a 1cm diameter hole in a steel sheet 0.3cm thick is nearly
A.1.4×104N1.4\times {{10}^{4}}N
B.2.7×104N2.7\times {{10}^{4}}N
C.3.3×104N3.3\times {{10}^{4}}N
D.1.1×104N1.1\times {{10}^{4}}N

Explanation

Solution

Recall that the shear stress just like any other stress is the force applied per unit area, but the force applied here is tangential. While punching a hole, the force is acting on a minute cylindrical area of given diameter and height equal to the thickness of the sheet. Now you could find the area of this minute cylinder substitute along with the given value of shear stress in the express for shear stress to find the required force.
Formula used:
The expression for shear stress,
S=FAS=\dfrac{F}{A}

Complete step-by-step solution
We are given a steel sheet which on application of 3.5×108Nm−23.5\times {{10}^{8}}N{{m}^{-2}} ruptures. On applying a force F we are punching a hole of diameter 1cm on a steel sheet of 0.3cm thickness. We asked to find the force applied in Newton.
Let us recall what shear stress was. By definition, shear stress is the restoring force acting per unit area and is developed due to the application of a tangential force. Hence, this stress also has another name as tangential stress.
Just like any other stress, the magnitude of shear stress given by,
S=FAS=\dfrac{F}{A} ……………………….. (1)
Where F is the force applied normal to the area of cross-section A.
The SI unit of stress is Nm−2N{{m}^{-2}} or Pascal (Pa) and its dimensional formula is given by,
[S]=[MLT−2][L]2=[ML−1T−2]\left[ S \right]=\dfrac{\left[ ML{{T}^{-2}} \right]}{{{\left[ L \right]}^{2}}}=\left[ M{{L}^{-1}}{{T}^{-2}} \right]

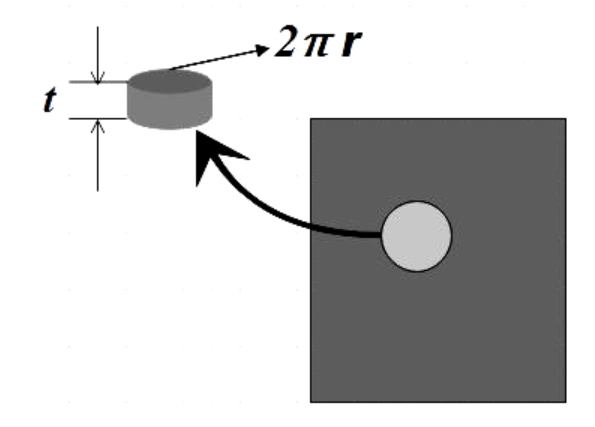
While we are making the hole on the sheet with thickness t, we are carving out a minute cylindrical part as shown in the figure. So the area on which the force is acting to cause shear stress and hence the rupture is that of a cylinder.
A = curved surface area of a cylinder =2πrt
We are given the diameter of the hole, d = 1cm, therefore, the radius of the hole will be,
r=d2=12=0.5cmr=\dfrac{d}{2}=\dfrac{1}{2}=0.5cm
Also, thickness t = 0.3cm
⇒A=2π×(0.5cm)×(0.3cm)\Rightarrow A=2\pi \times \left( 0.5cm \right)\times \left( 0.3cm \right)
⇒A=0.94cm2=0.94×10−4m2\Rightarrow A=0.94c{{m}^{2}}=0.94\times {{10}^{-4}}{{m}^{2}} …………………….. (2)
We are given the shear stress as,
S=3.5×108Nm−2S=3.5\times {{10}^{8}}N{{m}^{-2}} ………………………….. (3)
Substituting (2) and (3) in (1), we get,
⇒3.5×108Nm−2=F0.94×10−4m2\Rightarrow 3.5\times {{10}^{8}}N{{m}^{-2}}=\dfrac{F}{0.94\times {{10}^{-4}}{{m}^{2}}}
⇒F=3.5×0.94×104N\Rightarrow F=3.5\times 0.94\times {{10}^{4}}N
⇒F=3.29×104N≈3.3×104N\Rightarrow F=3.29\times {{10}^{4}}N\approx 3.3\times {{10}^{4}}N
Therefore, the force needed to punch a 1cm diameter hole in a steel sheet 0.3cm thick is near 3.3×104N3.3\times {{10}^{4}}N
Hence, the answer to the question is option C.

Note: Since the options are given in SI units, make sure that you convert the given quantities into their respective SI units. Also, while substituting for the area on which the force is acting, make sure that you also consider the thickness of the sheet. That is, you shouldn’t simply consider the circular area but instead, you should consider the minute cylindrical area.