Question
Question: The compressibility factor for 1 mole of a Vander Waal's gas Boyle temperature is...
The compressibility factor for 1 mole of a Vander Waal's gas Boyle temperature is
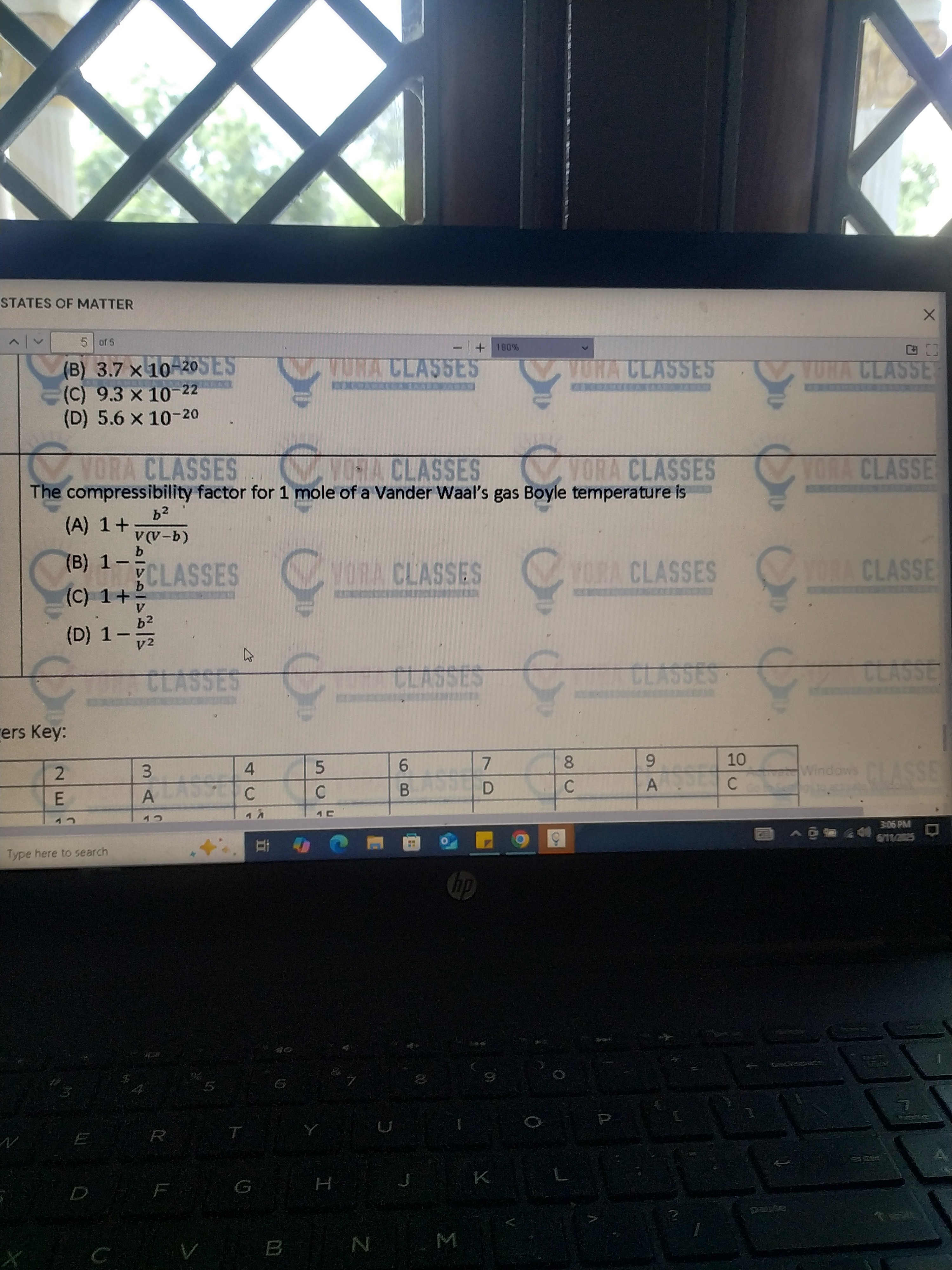
1+v(v−b)b2
1-vb
1+vb
1-v2b2
1+v(v−b)b2
Solution
The van der Waals equation for 1 mole of a real gas is given by:
(P+V2a)(V−b)=RT
The compressibility factor, Z, is defined as:
Z=RTPV
From the van der Waals equation, we can express pressure P:
P=V−bRT−V2a
Now, substitute this expression for P into the definition of Z:
Z=RT(V−bRT−V2a)V
Distribute V and divide by RT:
Z=(V−b)RTRT⋅V−V2RTaV
Z=V−bV−VRTa
The Boyle temperature (TB) is the temperature at which the second virial coefficient of a real gas is zero. For a van der Waals gas, the virial expansion of Z is:
Z=1+(b−RTa)V1+V2b2+…
The second virial coefficient is B=b−RTa. At Boyle temperature, B=0:
b−RTBa=0
RTBa=b
So, RTB=ba
Now, substitute RT=ba (since T=TB) into the expression for Z:
Z=V−bV−V(ba)a
Z=V−bV−Vb
To simplify, combine the terms on the right-hand side:
Z=V(V−b)V⋅V−b(V−b)
Z=V(V−b)V2−bV+b2
This can be rewritten by separating the first term:
Z=V−bV−Vb
We can write V−bV as V−bV−b+b=1+V−bb.
So,
Z=1+V−bb−Vb
Now combine the last two terms:
Z=1+(V−bb−Vb)
Z=1+(V(V−b)bV−b(V−b))
Z=1+(V(V−b)bV−bV+b2)
Z=1+V(V−b)b2
Comparing this with the given options, option (A) matches our result.
