Question

Statement – 1: The diagonals of the quadrilateral whose sides are 3x+2y+1=0 , 3x+2y+2=0, 2x+3y+1=0 and 2x+3y+2=0 include an angle $90^\circ$ .
Statement – 2: Diagonals of a parallelogram bisect each other.
A. Statement – 1 is true, statement – 2 is true; statement – 2 is a correct explanation for statement – 1
B. Statement – 1 is true, statement – 2 is true; statement – 2 is a not a correct explanation for statement – 1
C. Statement – 1 is true, statement – 2 is false
D. Statement – 1 is false, statement – 2 is true.

Answer 1

Hint – In this question first find out which lines are parallel to each other using slope concept i.e. parallel lines slope is equal to each other than calculate the intersection points of this lines using any method later on use the concept that two lines are perpendicular to each other if the slope multiplication is equal to (-1) later on use the concept of midpoint formula which is given as for two points $\left( {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2}} \right)$ so use these concepts to reach the solution of the question.

Complete step-by-step answer:

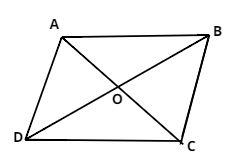
Given sides of a quadrilateral
$3x + 2y + 1 = 0.............\left( 1 \right) \\\ 3x + 2y + 2 = 0............\left( 2 \right) \\\ 2x + 3y + 1 = 0.............\left( 3 \right) \\\ 2x + 3y + 2 = 0............\left( 4 \right) \\\$
As we know for linear equation ax + by + c = 0 the slope is the ratio of negative times x coefficient to coefficient of y.
So slope of equation (1) is
$\Rightarrow {m_1} = \dfrac{{ - 3}}{2}$
The slope of equation (2) is
$\Rightarrow {m_2} = \dfrac{{ - 3}}{2}$
The slope of equation (3) is
$\Rightarrow {m_3} = \dfrac{{ - 2}}{3}$
And the slope of equation (4) is
$\Rightarrow {m_4} = \dfrac{{ - 2}}{3}$
So as we see that slope $\left( {{m_1}{\text{ and }}{m_2}} \right)$ are equal and slope $\left( {{m_3}{\text{ and }}{m_4}} \right)$ are equal.
So the quadrilateral ABCD is shown above having diagonals AC and BD.
Let AB = $3x + 2y + 1 = 0$................... (5)
BC = $2x + 3y + 1 = 0$........................ (6)
CD = $3x + 2y + 2 = 0$......................... (7)
DA = $2x + 3y + 2 = 0$...................... (8)
Therefore equation AB and CD are parallel to each other and similarly equation BC and DA are parallel to each other as shown in figure.
Let the diagonals intersect at the point O.
Now calculate the intersection point of lines.
So let the intersection point of AB and DA is $\left( {{x_1},{y_1}} \right)$
Now multiply by 2 in equation (5) and multiply by 3 in equation (8) and subtract them we have,
$\Rightarrow 2\left( {3x + 2y + 1} \right) - 3\left( {2x + 3y + 2} \right) = 0$
$\Rightarrow - 5y - 4 = 0$
$\Rightarrow y = \dfrac{{ - 4}}{5}$
Now substitute this value in equation (5) we have,
$\Rightarrow 3x + 2\left( {\dfrac{{ - 4}}{5}} \right) + 1 = 0$
$\Rightarrow 3x = - 1 + \dfrac{8}{5} = \dfrac{3}{5}$
$\Rightarrow x = \dfrac{1}{5}$
Therefore intersection point $\left( {{x_1},{y_1}} \right)$ = (1/5, -4/5).
Similarly the intersection of DA and CD is $\left( {{x_2},{y_2}} \right)$
Now multiply by 2 in equation (7) and multiply by 3 in equation (8) and subtract them we have,
$\Rightarrow 2\left( {3x + 2y + 2} \right) - 3\left( {2x + 3y + 2} \right) = 0$
$\Rightarrow - 5y - 2 = 0$
$\Rightarrow y = \dfrac{{ - 2}}{5}$
Now substitute this value in equation (7) we have,
$\Rightarrow 3x + 2\left( {\dfrac{{ - 2}}{5}} \right) + 2 = 0$
$\Rightarrow 3x = - 2 + \dfrac{4}{5} = \dfrac{{ - 6}}{5}$
$\Rightarrow x = \dfrac{{ - 2}}{5}$
Therefore intersection point $\left( {{x_2},{y_2}} \right)$ = (-2/5, -2/5).
Similarly the intersection of CD and BC is $\left( {{x_3},{y_3}} \right)$
Now multiply by 3 in equation (6) and multiply by 2 in equation (7) and subtract them we have,
$\Rightarrow 3\left( {2x + 3y + 1} \right) - 2\left( {3x + 2y + 2} \right) = 0$
$\Rightarrow 5y - 1 = 0$
$\Rightarrow y = \dfrac{1}{5}$
Now substitute this value in equation (7) we have,
$\Rightarrow 3x + 2\left( {\dfrac{1}{5}} \right) + 2 = 0$
$\Rightarrow 3x = - 2 + \dfrac{{ - 2}}{5} = \dfrac{{ - 12}}{5}$
$\Rightarrow x = \dfrac{{ - 4}}{5}$
Therefore intersection point $\left( {{x_3},{y_3}} \right)$ = (-4/5, 1/5).
Similarly the intersection of BC and AB is $\left( {{x_4},{y_4}} \right)$
Now multiply by 2 in equation (5) and multiply by 3 in equation (6) and subtract them we have,
$\Rightarrow 2\left( {3x + 2y + 1} \right) - 3\left( {2x + 3y + 1} \right) = 0$
$\Rightarrow - 5y - 1 = 0$
$\Rightarrow y = - \dfrac{1}{5}$
Now substitute this value in equation (5) we have,
$\Rightarrow 3x + 2\left( { - \dfrac{1}{5}} \right) + 1 = 0$
$\Rightarrow 3x = - 1 + \dfrac{2}{5} = \dfrac{{ - 3}}{5}$
$\Rightarrow x = \dfrac{{ - 1}}{5}$
Therefore intersection point $\left( {{x_4},{y_4}} \right)$ = (-1/5, -1/5).
Now as we know that the slope of two points $\left( {{x_1},{y_1}} \right)$ and $\left( {{x_2},{y_2}} \right)$ is calculated as
$m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$
So the slope of diagonal AC is
A = $\left( {{x_1},{y_1}} \right)$ = (1/5, -4/5).
C = $\left( {{x_3},{y_3}} \right)$ = (-4/5, 1/5).
$\Rightarrow {m_1} = \dfrac{{{y_3} - {y_1}}}{{{x_3} - {x_1}}} = \dfrac{{\dfrac{1}{5} - \dfrac{{ - 4}}{5}}}{{\dfrac{{ - 4}}{5} - \dfrac{1}{5}}} = \dfrac{{\dfrac{5}{5}}}{{\dfrac{{ - 5}}{5}}} = - 1$
Similarly the slope of diagonal BD is
B = $\left( {{x_4},{y_4}} \right)$ = (-1/5, -1/5).
D = $\left( {{x_2},{y_2}} \right)$ = (-2/5, -2/5).
$\Rightarrow {m_2} = \dfrac{{{y_2} - {y_4}}}{{{x_2} - {x_4}}} = \dfrac{{\dfrac{{ - 2}}{5} - \dfrac{{ - 1}}{5}}}{{\dfrac{{ - 2}}{5} - \dfrac{{ - 1}}{5}}} = \dfrac{{\dfrac{{ - 1}}{5}}}{{\dfrac{{ - 1}}{5}}} = 1$
So the product of slopes is
$\Rightarrow {m_1}.{m_2} = - 1$
Which is the required condition that the diagonals of the parallelogram include an angle $\dfrac{\pi }{2}$ or $90^\circ$.
So the statement – 1 is true.
Now the midpoint of diagonal AC is calculated as
$\Rightarrow M.{P_1} = \left( {\dfrac{{{x_1} + {x_3}}}{2},\dfrac{{{y_1} + {y_3}}}{2}} \right) = \left( {\dfrac{{\dfrac{1}{5} + \dfrac{{ - 4}}{5}}}{2},\dfrac{{\dfrac{{ - 4}}{5} + \dfrac{1}{5}}}{2}} \right) = \left( {\dfrac{{ - 3}}{{10}},\dfrac{{ - 3}}{{10}}} \right)$

And the midpoint of diagonal BD is calculated as
$\Rightarrow M.{P_2} = \left( {\dfrac{{{x_4} + {x_2}}}{2},\dfrac{{{y_4} + {y_2}}}{2}} \right) = \left( {\dfrac{{\dfrac{{ - 1}}{5} + \dfrac{{ - 2}}{5}}}{2},\dfrac{{\dfrac{{ - 1}}{5} + \dfrac{{ - 2}}{5}}}{2}} \right) = \left( {\dfrac{{ - 3}}{{10}},\dfrac{{ - 3}}{{10}}} \right)$
So as we see both the midpoints are equal which intersects at point O as shown in figure.
So OA = OC and OB = OD
Therefore diagonals of the parallelogram bisect each other.
Therefore statement – 2 is also true but not a correct explanation of statement – 1.
Hence option (B) is correct.

Note – There are different concepts to solve linear equations such as (substitution, elimination, cross-multiplication etc.) so here we use substitution method so first using slope concept and find out which line is parallel to each other as above then use substitution method to get the intersection points of these lines then calculate the slope of the diagonals if the lope multiplication of these diagonal is (-1) then the diagonals are perpendicular to each other than calculate the midpoint of these diagonals if the midpoint of these diagonals are equal then the diagonals of the parallelogram are bisect to each other.