Question

Statement-1: If the middle point of the sides of a triangle ABC are ( 0,0), ( 1,2), ( -3,4) then centroid of $\Delta ABC$ is $\left( \dfrac{-2}{3},2 \right)$.
Statement-2: Centroid of a triangle ABC and centroid of the triangle formed by joining the mid points of sides of triangle ABC be always the same .
A) Statement $-1$ is True. Statement $-2$ True: Statement $-2$ is a correct explanation for statement$-1$.
B) Statement $-1$ is True. Statement $-2$ True: Statement $-2$ is not correct explanation for statement $-1$
C) Statement $-1$ is True. Statement $-2$ False
D) Statement $-1$ is False. Statement $-2$ True

Answer 1

Hint: The coordinates of centroid of a triangle with vertices $\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right),\left( {{x}_{3}},{{y}_{3}} \right)$ is given as $\left( \dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},\dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3} \right)$ .

Statement-1: The given triangle is $\Delta ABC$. We will consider the vertices of $\Delta ABC$ to be given as $A\left( {{x}_{1}},{{y}_{1}} \right),B\left( {{x}_{2}},{{y}_{2}} \right)\ and C\left( {{x}_{3}},{{y}_{3}} \right)$.

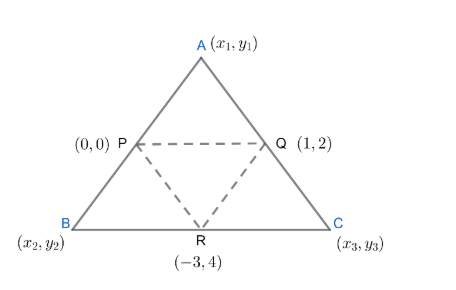
Now , from the diagram , we can see that $P,Q,R$ are the midpoints of sides $AB,AC$ and $BC$ respectively .
Now , we know that the midpoint of line joining $\left( {{a}_{1}},{{b}_{1}} \right)\ and \left( {{a}_{2}},{{b}_{2}} \right)$ is given as
$\left( \dfrac{{{a}_{1}}+{{a}_{2}}}{2},\dfrac{{{b}_{1}}+{{b}_{2}}}{2} \right)$
So , midpoint of $AB$ i.e., $P$ is given as
$\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$
But , in the question , it is given that coordinates of $P$ are $\left( 0,0 \right)$.
So , $\dfrac{{{x}_{1}}+{{x}_{2}}}{2}=0\Rightarrow {{x}_{1}}+{{x}_{2}}=0.........\left( i \right)$
And $\dfrac{{{y}_{1}}+{{y}_{2}}}{2}=0\Rightarrow {{y}_{1}}+{{y}_{2}}=0.........\left( ii \right)$
Again , midpoint of $AC$ is $Q$. So , the coordinates of $Q$ are given as
$\left( \dfrac{{{x}_{1}}+{{x}_{3}}}{2},\dfrac{{{y}_{1}}+{{y}_{3}}}{2} \right)$
But in the question, coordinates of $Q$ are given as $\left( 1,2 \right)$.
So , $\begin{aligned} & \dfrac{{{x}_{1}}+{{x}_{3}}}{2}=1\Rightarrow {{x}_{1}}+{{x}_{3}}=2......\left( iii \right) \\\ & \\\ \end{aligned}$
And $\dfrac{{{y}_{1}}+{{y}_{2}}}{2}=2\Rightarrow {{y}_{1}}+{{y}_{3}}=4........\left( iv \right)$
Again , midpoint of $BC$ is $R$. So , the coordinates of $R$ are given as
$\left( \dfrac{{{x}_{2}}+{{x}_{3}}}{2},\dfrac{{{y}_{2}}+{{y}_{3}}}{2} \right)$
But in the question, coordinates of $R$ are given as $\left( -3,4 \right)$.
So, $\dfrac{{{x}_{2}}+{{x}_{3}}}{2}=-3\Rightarrow {{x}_{2}}+{{x}_{3}}=-6..........\left( v \right)$
And $\dfrac{{{y}_{2}}+{{y}_{3}}}{2}=4\Rightarrow {{y}_{2}}+{{y}_{3}}=8..........\left( vi \right)$
Now , we will add the equations $\left( i \right),\left( iii \right)$ and $\left( v \right)$.
On adding equations $\left( i \right),\left( iii \right)$ and $\left( v \right)$ , we get
$\begin{aligned} & {{x}_{1}}+{{x}_{2}}+{{x}_{1}}+{{x}_{3}}+{{x}_{2}}+{{x}_{3}}=0+2+\left( -6 \right) \\\ & \Rightarrow 2\left( {{x}_{1}}+{{x}_{2}}+{{x}_{3}} \right)=-4 \\\ & \Rightarrow \left( {{x}_{1}}+{{x}_{2}}+{{x}_{3}} \right)=-2...........\left( vii \right) \\\ \end{aligned}$
Now , we will add the equations $\left( ii \right),\left( iv \right)$and $\left( vi \right)$.
On adding equations $\left( ii \right),\left( iv \right)$and $\left( vi \right)$, we get
$\begin{aligned} & {{y}_{1}}+{{y}_{2}}+{{y}_{1}}+{{y}_{3}}+{{y}_{2}}+{{y}_{3}}=0+4+8 \\\ & \Rightarrow 2\left( {{y}_{1}}+{{y}_{2}}+{{y}_{3}} \right)=12 \\\ & \Rightarrow \left( {{y}_{1}}+{{y}_{2}}+{{y}_{3}} \right)=6...................\left( viii \right) \\\ \end{aligned}$
Now , we know the coordinates of centroid of a triangle with vertices $\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right),\left( {{x}_{3}},{{y}_{3}} \right)$ is given as $\left( \dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},\dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3} \right)$ .
So , the coordinates of centroid of $\Delta ABC$is
$G\left( \dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},\dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3} \right)$
But , from equations $\left( vii \right)$and $\left( viii \right)$, we have
${{x}_{1}}+{{x}_{2}}+{{x}_{3}}=-2$ and ${{\text{y}}_{1}}+{{y}_{2}}+{{y}_{3}}=6\text{ }$
So , coordinates of the centroid of $\Delta ABC$are $G\left( \dfrac{-2}{3},2 \right)$ .
Hence , the statement $\left( 1 \right)$ is true.
Statement $2$: Let the vertices of triangle be $A\left( {{x}_{1}},{{y}_{1}} \right),B\left( {{x}_{2}},{{y}_{2}} \right)\And C\left( {{x}_{3}},{{y}_{3}} \right)$
So the midpoint of $AB$ is $D\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$ , $\text{BC}$ is $\text{E}\left( \dfrac{{{x}_{2}}+{{x}_{3}}}{2},\dfrac{{{y}_{2}}+{{y}_{3}}}{2} \right)$ and $AC$ is $\text{F}\left( \dfrac{{{x}_{1}}+{{x}_{3}}}{2},\dfrac{{{y}_{1}}+{{y}_{3}}}{2} \right)$.

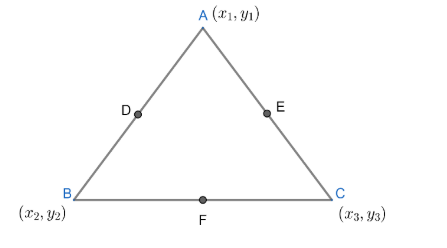
Now , we will find the centroid of $\Delta ABC$.
We know the coordinates of centroid of a triangle with vertices $\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right),\left( {{x}_{3}},{{y}_{3}} \right)$ is given as $\left( \dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},\dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3} \right)$.
So , the centroid of $\Delta ABC$ is $\left( \dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},\dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3} \right)$ .
Now , we will find the centroid of $\Delta DEF$.
The centroid of $\Delta DEF$ is given as $\left( \dfrac{\dfrac{{{x}_{1}}+{{x}_{2}}}{2}+\dfrac{{{x}_{2}}+{{x}_{3}}}{2}+\dfrac{{{x}_{3}}+{{x}_{1}}}{2}}{3},\dfrac{\dfrac{{{y}_{1}}+{{y}_{2}}}{2}+\dfrac{{{y}_{3}}+{{y}_{2}}}{2}+\dfrac{{{y}_{1}}+{{y}_{3}}}{2}}{3} \right)$
$=\left( \dfrac{\dfrac{2\left( {{x}_{1}}+{{x}_{2}}+{{x}_{3}} \right)}{2}}{3},\dfrac{\dfrac{2\left( {{y}_{1}}+{{y}_{2}}+{{y}_{3}} \right)}{2}}{3} \right)$
$=\left( \dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},\dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3} \right)$
= centroid of $\Delta ABC$.
Hence , the statement $\left( 2 \right)$ is true.
So , we can conclude that statement $\left( 1 \right)$ is true, statement $\left( 2 \right)$ is true and statement $\left( 2 \right)$ is a correct explanation for statement$\left( 1 \right)$.
So, (1) Statement $\left( 1 \right)$ is true, statement $\left( 2 \right)$ is true; statement $\left( 2 \right)$ is a correct explanation for statement $\left( 1 \right)$.

Note: The midpoint of line joining the points $\left( {{x}_{1}},{{y}_{1}} \right)\text{ and }\left( {{x}_{2}},{{y}_{2}} \right)$ is given as:
$\left( \dfrac{\left( {{x}_{1}}+{{x}_{2}} \right)}{2},\dfrac{\left( {{y}_{1}}+{{y}_{2}} \right)}{2} \right)$ and not $\left( \dfrac{\left( {{x}_{1}}-{{x}_{2}} \right)}{2},\dfrac{\left( {{y}_{1}}-{{y}_{2}} \right)}{2} \right)$ . Students often get confused between the two. Due to this confusion , they generally end up getting a wrong answer . So , such mistakes should be avoided .