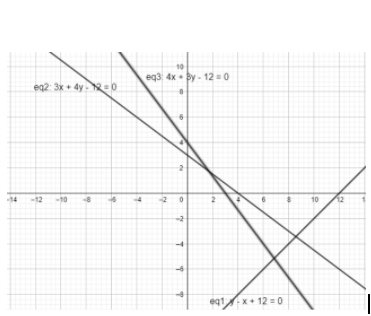
Question

Statement-1 : Each point on the line $y-x+12=0$ is at the same distance from the lines $3x+4y-12=0$ and $4x+3y-12=0$ .
Statement-2 : Locus of point which is at equal distance from the two given intersecting lines is the angle bisectors of the two lines.
(a). Statement-1 is true, Statement-2 is true; Statement-2 is a correct explanation for Statement-1.
(b). Statement-1 is true, Statement-2 is true; Statement-2 is NOT a correct explanation for Statement-1
(c). Statement-1 is true, Statement-2 is False
(d). Statement-1 is False, Statement-2 is true

Answer 1

First find the intersection point of 2 lines. See if a given line is passing through this point or not. If it passes then as it is given equidistance the perpendicular distances will be the same. So the value of sin of angle between lines will be perpendicular / hypotenuse which will turn out to be the same. As angle is same it is concluded as angle of bisector.

Complete step-by-step answer :
If two lines form an angle then they have 2 angle bisectors because 2 lines there are 2 angles possible which are acute and obtuse. So, the 2 lines bisecting these 2 angles between lines $ax+by+c=0$ and $dx+ey+f=0$ is given by
$\dfrac{ax+by+c}{\sqrt{{{a}^{2}}+{{b}^{2}}}}=\pm \dfrac{dx+ey+f}{\sqrt{{{d}^{2}}+{{f}^{2}}}}$
So, the symbol plus or minus denotes 2 equations of bisectors. Out of both any of them may be acute and may be obtuse. If one is acute then the other is obtuse and vice versa.
As told before the 2 bisectors are given like this:

As the angles are same the perpendicular will be equal because ${{90}^{\circ }}$ is same, hypotenuse is same and as it is angle bisector bisected angles are same.
So, by ASA axiom we can say the distance of line from 2 lines is the same.
So, the locus of points which is equidistant from 2 lines is angular bisector.
In given question line equations are $3x+4y-12=0$ , $4x+3y-12=0$
The first line equation given in the question can be written as:
3x + 4y – 12 = 0
By substituting x = 0, we get the value of y as:
3(0) + 4y – 12 = 0
By simplifying the above equation, we get the value of y as:
4y = 12
By dividing with 4 on both sides, we get value of y as:
y = 3
By substituting y = 0 value in the equation, we get it as:
3x + 4(0) – 12 = 0
By simplifying the above equation, we get the value of x as:
3x = 12
By dividing with 3 on both sides, we get value of y as:
x = 4
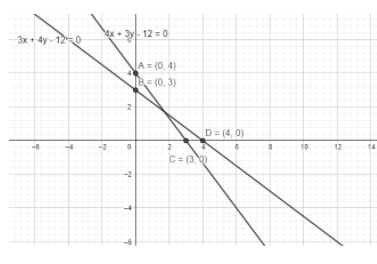
The points (4, 0) and (0, 3) are the two points on axes through which the first line passes.
The second line equation given in the question can be written as:
4x + 3y – 12 = 0
By substituting x = 0, we get the value of y as:
4(0) + 3y – 12 = 0
By simplifying the above equation, we get the value of y as:
3y = 12
By dividing with 3 on both sides, we get value of y as:
y = 4
By substituting y = 0 value in the equation, we get it as:
4x + 3(0) – 12 = 0
By simplifying the above equation, we get the value of x as:
4x = 12
By dividing with 4 on both sides, we get value of y as:
x = 3
The points (3, 0) and (0, 4) are the two points on axes through which the second line passes.

Applying angular bisector formula, we get:
$\dfrac{3x+4y-12}{\sqrt{{{3}^{2}}+{{y}^{2}}}}=\pm \dfrac{4x+3y-12}{\sqrt{{{3}^{2}}+{{y}^{2}}}}$
By simplifying we get-
$x-y=0$ : $7x+7y-24=0$
So, the given equation $y-x+12=0$ is not locus.
Statement-1 is wrong but Statement-2 is true.
Option (D) is the correct answer for the question.

Note :Do observe carefully the plus or minus sign in angular bisector formula. If you miss the sign you will miss 1 equation of a bisector out of 2 you get only 1.
Alternate method-
By graph we can directly say it is not an angular bisector, we can see the difference in distances directly.