Question

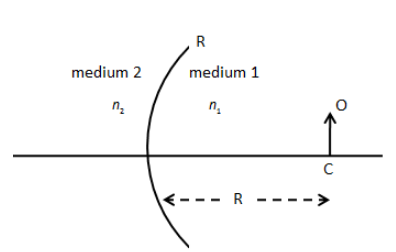
STATEMENT-1: A spherical surface of radius of curvature R separates two media of refractive index ${n_1}$ and ${n_2}$ as shown. If an object O (a thin small rod) is placed upright on the principal axis at a distance R from pole (i.e., placed at centre of curvature), then the size of image is different from size of object.
STATEMENT-2: If a point object is placed at centre of curvature of spherical surface separating two media of different refractive index, then the image is also formed at centre of curvature, i.e. image distance is equal to object distance.

A. Both statement-1 and statement-2 are true; statement-2 is the correct explanation for statement-1.
B. Both statement-1 and statement-2 are true but statement-2 is not a correct explanation for statement-1.
C. Statement-1 is true but statement-2 is false.
D. Statement-1 is false but statement-2 is true.

Answer 1

A concave mirror can form both real and virtual images of the object depending on the position of the object from the plane of the mirror. If the object is placed at the curvature of the mirror, the image of the object also forms at the curvature of the mirror but the image is inverted. Use the formula for magnification of the mirror to determine the size of the mirror as compared to the size of the object.

Complete step by step answer:
Let’s recall the characteristics of the concave mirror. We know that the concave mirror is capable of producing both real and virtual images of the object depending on the position of the object from the plane of the mirror. If the object is placed beyond the focal length of the concave mirror, the real image is produced while if the object is placed closer to the mirror than the focal length, the virtual image of the object is produced.

If the object is placed at the curvature of the mirror, the image of the object also forms at the curvature of the mirror but the image is inverted. Therefore, we can see that the image distance is equal to the object distance. Therefore, the statement-2 is true.
We have the formula for the magnification of the image by the mirror,
$m = - \dfrac{v}{u}$
Here, v is the image distance and u is the object distance.

Since we have the image distance is equal to the object distance, the magnification of the image will be,
$m = - \dfrac{u}{u}$
$\therefore m = - 1$
The magnification $- 1$ implies that the height of the image is the same as the height of the object and the image is inverted. Therefore, the statement-1 is false.

The different refractive indices on the inner and outer side of the mirror will not affect the magnification because the light rays do not refract in the case of spherical mirrors.

So, the correct answer is option D.

Note: In case of spherical lenses, the height of the image would have been affected due to different refractive indices on the both sides of the lens because in the case of spherical lenses, the image forms due to refraction of light rays. In the case of the spherical mirrors, the outer or inner surface of the mirror is painted black to undergo light reflection. We know that the virtual image forms on the opposite side of the object. In this case, remember, the light rays do not undergo refraction through the mirror.