Question
Question: State whether the two lines through (9,5) and (-1,1) and through (3,-5) and (8,-3) are parallel, per...
State whether the two lines through (9,5) and (-1,1) and through (3,-5) and (8,-3) are parallel, perpendicular or neither.
Solution
Hint: Find the slope of the lines using the property that the slope of the line joining the points A(x1,y1) and B(x2,y2) is given by m=x2−x1y2−y1. Use the fact that if the slopes of two lines are equal, then they are parallel to each other and if the product of the slopes of two lines is -1, then the lines are perpendicular. Hence determine whether the lines are parallel or perpendicular or neither.
Complete step-by-step answer:
Finding the slope of the line joining (9,5) and (-1,1):
We know that the slope of the line joining the points A(x1,y1) and B(x2,y2) is given by m=x2−x1y2−y1.
Here x1=9,x2=−1,y1=5 and y2=1
Hence the slope of the line is m=−1−91−5=−10−4=52
Finding the slope of the line joining (3,-5) and (8,-3):
We know that the slope of the line joining the points A(x1,y1) and B(x2,y2) is given by m=x2−x1y2−y1.
Here x1=3,x2=8,y1=−5 and y2=−3
Hence the slope of the line is m=8−3−3−(−5)=52
Now since the slope of the line joining (9,5) and (-1,1) is equal to the slope of the line joining (3,-5) and (8,-3), the lines are parallel to each other.
Note: [i] Viewing graphically:
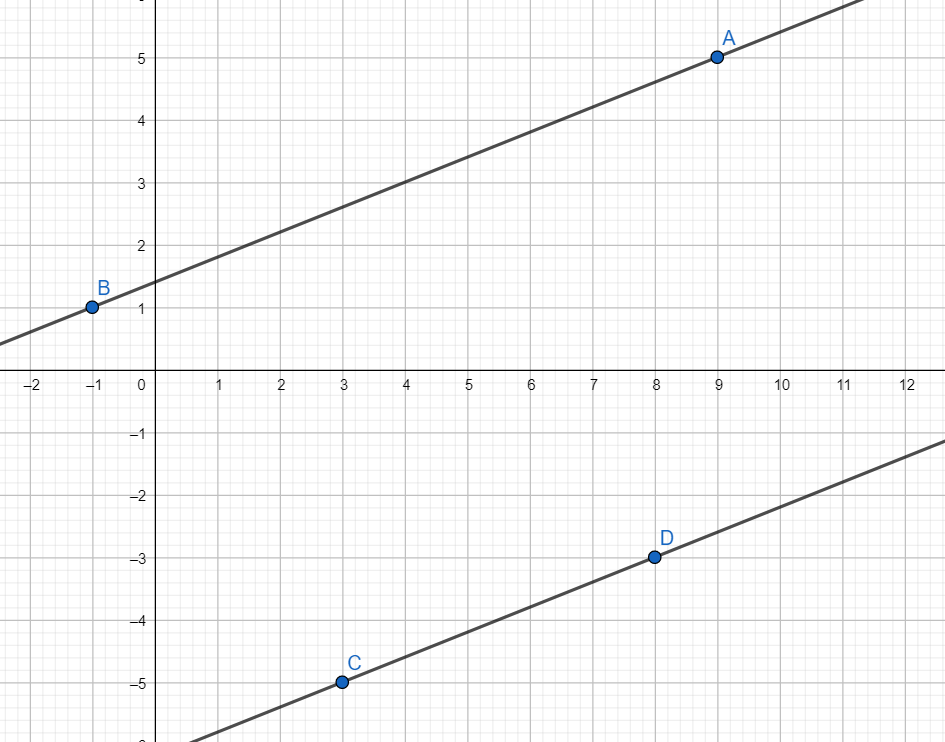
As is evident from the graph AB∥CD
[ii] Alternative solution:
Let the equation of AB be y=mx+c
Since the line passes through (9,5), we have
9m+c=5
Also, since the line passes through (-1,1), we have
−m+c=1
Hence, we have
9m+m=5−1⇒m=104=52
Hence the slope of AB is 52
Let the equation of CD be y = mx+c
Since the line passes through (3,-5), we have
3m+c=−5
Also, since the line passes through (8,-3), we have
8m+c=−3
Hence, we have
8m−3m=−3+5⇒m=52
Hence the slope of CD is 52
Hence the lines are parallel to each other.
