Question

State whether the given statement is true or false:
In an AC circuit the power across the load is maximum/peaks at a frequency where the load impedance is the complex conjugate of the output impedance.
(A) TRUE
(B) FALSE

Answer 1

This question is based upon maximum power transfer theorem, which states that for DC circuits, power transferred from source to load is maximum when value of load resistance is equal to source resistance. And for AC circuits power transferred from source to load is maximum when value of load impedance is complex conjugate of source impedance.Now, for finding this result take a circuit with both source and load having resistance and reactance components. Then find the current I in the circuit using ohm’s law: V = IR.
After finding I, find power across the load using formula: P = I2R.
For finding the maxima of P equate $\dfrac{{\delta {P_L}}}{{\delta {X_L}}} = 0$, where XL is the load reactance, you will get some relation put back it in equation of power.
And again equate $\dfrac{{d{P_L}}}{{d{R_L}}} = 0$, where RL is load resistance.
In this way you will find conditions for maximum power transfer, i.e. load impedance is complex conjugate of source impedance.

Complete step by step answer:
According to maximum power transfer theorem:
For DC circuits: The power transferred to the load is maximum when the load resistance is equal to source resistance.

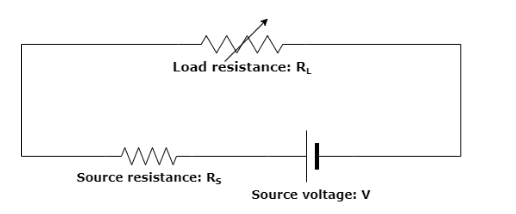
I.e. ${R_L} = {R_S}$ .
For AC circuits: The maximum power transferred to the load is maximum when the load impedance is equal to the complex conjugate of source impedance.

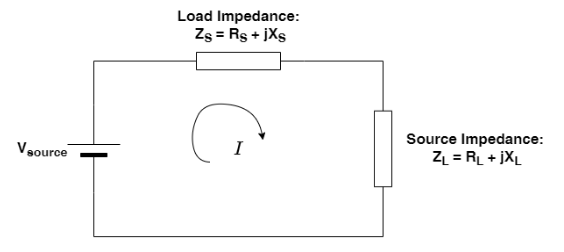
That is:
${Z_S} = \overline {{Z_L}} \\\ \Rightarrow {R_S} + j{X_S} = {R_L} - j{X_L} \\\ \therefore {R_S} = {R_L}{\text{ and }}{X_S} = - {X_L} \\\$
Which means, load resistance is equal to source resistance and load reactance is negative of source reactance.
So, from the maximum power transfer theorem the given statement is true.
Additional Information:
Proof of maximum power transfer theorem:
Consider a circuit having Load impedance which has both varying resistance and varying reactance. The current flowing through the circuit across the load terminals is given as:
${\text{Current = }}\dfrac{{{\text{Source voltage}}}}{{{\text{Total Impedance}}}} \\\ \Rightarrow I = \dfrac{{{V_S}}}{{{Z_S} + {Z_L}}} \\\$
Where,

$${{Z_L} = {R_L}\; + {\text{ }}j{X_L}} \\\ \Rightarrow{{Z_S}\; = {\text{ }}{R_{S\;}} + {\text{ }}j{X_S}}$$

The notation $Z = R + jX$, is nothing but complex notation for impedance, where R is resistance and X is reactance (sum of inductance and capacitance) .
Therefore,

$${I{\text{ }} = {\text{ }}\dfrac{{{V_S}}}{{\left( {{R_L}\; + {\text{ }}j{X_L}\; + {\text{ }}{R_{S\;}} + {\text{ }}j{X_{S\;}}} \right)}}\;} \\\ { \Rightarrow I = {\text{ }}\dfrac{{{V_S}}}{{\left( {\left( {{R_L} + {\text{ }}{R_S}} \right){\text{ }} + {\text{ }}j\left( {{X_L}\; + {\text{ }}{X_{S\;}}} \right)} \right)}}}$$

The power delivered to the load will be:

$${{P_{L\;}} = {\text{ }}{I^{2\;}}{R_L}} \\\ \Rightarrow{P_{L\;}} = {\text{ }}\;\dfrac{{V_S^2}}{{\left( {{{\left( {{R_L} + {\text{ }}{R_{TH}}} \right)}^{2\;}} + {\text{ }}{{\left( {{X_L}\; + {\text{ }}{X_{TH\;}}} \right)}^2}} \right)}} \times {{\text{R}}_L} \\\ \Rightarrow{P_L} = \dfrac{{V_S^2 \times {R_L}}}{{\left( {{{\left( {{R_L} + {\text{ }}{R_{TH}}} \right)}^{2\;}} + {\text{ }}{{\left( {{X_L}\; + {\text{ }}{X_{TH\;}}} \right)}^2}} \right)}} - - - - - - - - - \left( 1 \right) \\\$$

For finding maxima of power we put the derivative of the above equation to be zero
I.e. $\dfrac{{\delta {P_L}}}{{\delta {X_L}}} = 0$
After simplification we get

$${{X_L}\; + {\text{ }}{X_{S\;}} = {\text{ }}0} \\\ \Rightarrow{{X_L}\; = {\text{ }}-{\text{ }}{X_S}}$$

Putting the above relation in eq.(1), we get:
${P_{L\;}} = {\text{ }}\dfrac{{V_S^2 \cdot \;{R_L}}}{{{{\left( {{R_L} + {\text{ }}{R_{S\;}}} \right)}^2}}}$
Again, for maximum power transfer, the derivative of above equation must be equal to zero
I.e. $\dfrac{{d{P_L}}}{{d{R_L}}} = 0$
After simplification, we get:

$${{R_L} + {\text{ }}{R_{S\;}} = {\text{ }}2{\text{ }}{R_L}} \\\ \Rightarrow{{R_{L\;}} = {\text{ }}{R_S}}$$

Hence, the maximum power will be transferred from source to the load:
if ${R_L}{\text{ }} = {\text{ }}{R_S}$ and ${X_L}{\text{ }} = {\text{ }}-{\text{ }}{X_S}$ in an AC circuit.
This means that the load impedance should be equal to the complex conjugate of source impedance of the circuit:
I.e. ${Z_L}\; = {\text{ }}\overline {{Z_S}}$
This maximum power transferred will be:
$\;{P_{max}}\; = {\text{ }}\dfrac{{V_S^2\;}}{{4{\text{ }}{R_S}\;}}{\text{ or }}\dfrac{{V_S^2\;}}{{4{\text{ }}{R_L}\;}}$--------------(2)

Note: The efficiency of the network at maximum power transfer conditions is 50%.
Since, Input power is :
${P_{input}} = \dfrac{{{{\left( {{\text{source voltage}}} \right)}^2}}}{{{\text{Total resistance of the circuit}}}} \\\ \Rightarrow {P_{input}} = \dfrac{{V_S^2}}{{{R_L} + {R_S}}} = \dfrac{{V_S^2}}{{2{R_L}}}{\text{ }}\left( {\because {{\text{R}}_L} = {R_S}} \right) \\\$
Output power across load is:
${P_{output}} = \dfrac{{V_S^2}}{{4{R_L}}}{\text{ }}\left( {{\text{from (2)}}} \right)$
$Efficiency = \dfrac{{{P_{output}}}}{{{P_{input}}}} \times 100 = \dfrac{{\left( {\dfrac{{{{V_S^2}}}}{{4{{{R_L}}}}}} \right)}}{{\left( {\dfrac{{{{V_S^2}}}}{{2{{{R_L}}}}}} \right)}} \times 100 = \dfrac{2}{4} \times 100 = 50\%$