Question

State whether the following statement is true or false. Justify your answer.
The set of all integers is contained in the set of all rational numbers.
${\text{(A)}}$True
${\text{(B)}}$False

Answer 1

Hint:- Use Venn’s Diagram.

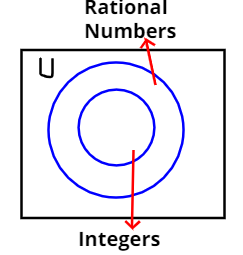
As we know that,
A rational number is of the form $\dfrac{p}{q}$ where q is not equal to zero.
So, some rational numbers will be $\dfrac{{ - 5}}{3},\dfrac{2}{5},\dfrac{1}{7},\dfrac{5}{1},\dfrac{{ - 3}}{1}$etc.
And, integer is a whole number (not a fractional number) that can be positive, negative, or zero.
As if we take, $q = 1$ then every rational number will become integer.
And we know any set X is contained in any other set Y if all elements of X also belong to Y.
So, every integer number is written as a rational number with q=1.
Hence, the statement is true. The set of all integers is contained in the set of all rational numbers.

Note:- Whenever we came up with this type of problem then we should go with the
definition of rational numbers, integers, whole numbers and non-rational numbers.
It will be the easiest and efficient way to prove the result.