Question

State true or false.
If the length of the shadow of a tower is increasing, then the angle of elevation of the sun is also increasing.

Answer 1

The tower stands on the ground making an angle $90^ \circ$. Thus the tower, the shadow of the tower and the line joining the free end of the tower and its shadow make a right angled triangle and the angle of elevation is the that is in the front of the tower. First we will derive tan of angle of elevation for 3 of the distance cases. Then from their value in terms of distance we will obtain the relation between angle of elevations.

Complete step-by-step answer:
Representing the tower length, length of the shadow of the tower and angle of elevation in a diagram below,

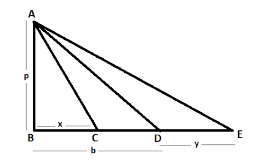
In the right angled triangle ABE,
Let the length of the tower be ‘p’
And the length of the shadow be ‘b’ and let the angle of elevation be $\angle ADB = \theta$
For the shadow length ‘x’, angle of elevation be $\angle ACB = {\theta _1}$
For the shadow length ‘b + y’, angle of elevation be $\angle AEB = {\theta _2}$
From the diagram,
$\tan \theta = \dfrac{p}{b}$ , $\tan {\theta _1} = \dfrac{p}{x}$ , $\tan {\theta _2} = \dfrac{p}{{b + y}}$
As x, b, b + y are distances, they are greater than zero
Hence b>0, x>0, b + y>0
As y is positive, $$
$\Rightarrow \dfrac{p}{{b + y}} < \dfrac{p}{b}$
$\tan {\theta _2} < \tan \theta$
$\Rightarrow {\theta _2} < \theta$ -------(1)
Similarly we can prove $\theta < {\theta _1}$ --------(2)
From equation (1) and (2) we get that,
${\theta _1} > \theta > {\theta _2}$
Hence it is concluded that if the length of the shadow of a tower is increasing, then the angle of elevation of the sun is decreasing.

The given statement is false.

Note: Be cautious while comparing angles with the length of the shadow of the tower.
Angle of elevation is the upward angle from the horizontal to a line of sight from the observer to some point of interest.
We can find the angle of elevation using trigonometric function tan. i.e. in a right angled triangle tan of angle of elevation is the ratio of perpendicular to the base of that right angled triangle.
Length of the shadow is inversely proportional to the angle of elevation.