Question

State True or False:
If the angle of elevation of a cloud from a point $h$ meters above a lake has measure $\alpha$ and the angle of depression of its reflection in the lake has measure $\beta$, then height of the cloud is $\dfrac{{h(\tan \alpha + \tan \alpha )}}{{\tan \beta - \tan \beta }}$.
A.True
B.False

Answer 1

We will first draw the diagram using the given information and mark the positions of the cloud and its reflection with respect to the lake. Then we will apply the trigonometric ratio to find appropriate relations between the angles $\alpha$ and $\beta$. Finally, we will find the height of the cloud in terms of the angles $\alpha$ and $\beta$, then compare it with the given height to state whether the statement is true or false.

Formula used:
If $\alpha$ is an acute angle in a right-triangle, then $\tan \alpha = \dfrac{{{\text{opposite side}}}}{{{\text{adjacent side}}}}$

Complete step-by-step answer:
Let $P$ be the position of the cloud and $P'$ be the position of the reflection of the cloud.
Let $O$ and $Q$ be the points $h$ meters above the lake. Let the cloud be $x$ meters above the lake.
Let $SR$ be the surface of the lake such that $OS = QR = h$ and $PR = P'R = x$. We have to find $x$.

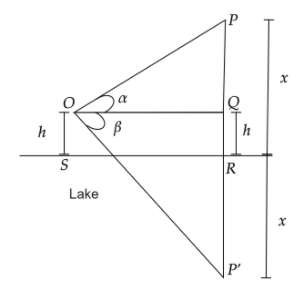
From the figure,
$PR = PQ + QR$
Substituting $QR = h$ in the above equation, we get
\Rightarrow x = PQ + h \\\ \Rightarrow PQ = x - h \\\
Also, $P'Q = P'R + RQ = x + h$
Now in $\vartriangle OPQ$,
$\tan \alpha = \dfrac{{PQ}}{{OQ}}$
Substituting $PQ = x - h$ in the above equation, we get
$\Rightarrow \tan \alpha = \dfrac{{x - h}}{{OQ}}$
Writing the above relation in terms of $OQ$, we get
$OQ = \dfrac{{x - h}}{{\tan \alpha }}$ ……………..$\left( 1 \right)$
Now, consider $\vartriangle OP'Q$
$\tan \beta = \dfrac{{P'Q}}{{OQ}}$
$\Rightarrow \tan \beta = \dfrac{{x + h}}{{OQ}}$
On cross multiplication, we get
$OQ = \dfrac{{x + h}}{{\tan \beta }}$ ……………..$\left( 2 \right)$
Now equating equation $\left( 1 \right)$ and $\left( 2 \right)$, we get
$\dfrac{{x - h}}{{\tan \alpha }} = \dfrac{{x + h}}{{\tan \beta }}$
On Cross multiplication, we get
$\Rightarrow$ $(x - h)\tan \beta = (x + h)\tan \alpha$
Multiplying the terms on the LHS and RHS, we have
$\Rightarrow$ $x\tan \beta - h\tan \beta = x\tan \alpha + h\tan \alpha$
Collecting the like terms on the LHS and RHS,
$\Rightarrow$ $x\tan \beta - x\tan \alpha = h\tan \alpha + h\tan \beta$
Taking $x$ common from the LHS and $h$ common from the RHS, we get
$\Rightarrow$ $x(\tan \beta - \tan \alpha ) = h(\tan \alpha + \tan \beta )$
Taking $(\tan \beta - \tan \alpha )$ to the denominator in the RHS, we get
$\Rightarrow$ $x = \dfrac{{h(\tan \alpha + \tan \beta )}}{{\tan \beta - \tan \alpha }}$
Thus, the height of the cloud is $\dfrac{{h(\tan \alpha + \tan \beta )}}{{\tan \beta - \tan \alpha }}$.
But we are given height of the cloud as $\dfrac{{h(\tan \alpha + \tan \alpha )}}{{\tan \beta - \tan \beta }}$, which is not the same as what we have found.
Hence, the given statement is False.

Note: If a person stands and looks up at an object, the angle of elevation is the angle between the horizontal line of sight and the object. If a person stands and looks down at an object, the angle of depression is the angle between the horizontal line of sight and the object. Here, it is important to draw the diagram so that we can easily find the length of each side of the triangle.