Question

State true or false for the given trigonometric expression $\cos 11{}^\circ -\cos 2{}^\circ >0$,
A. True
B. False

Answer 1

Hint: We will first calculate the value of $\cos 11{}^\circ$ and then we will calculate the value of $\cos 2{}^\circ$. Finally we will subtract the value of $\cos 2{}^\circ$with $\cos 11{}^\circ$ to get the final result.

Complete step-by-step answer:
It is given that we have to find the relation $\cos 11{}^\circ -\cos 2{}^\circ >0$ is true or false.
This picture and the values below the picture shows $\cos \theta$ values at different angles.

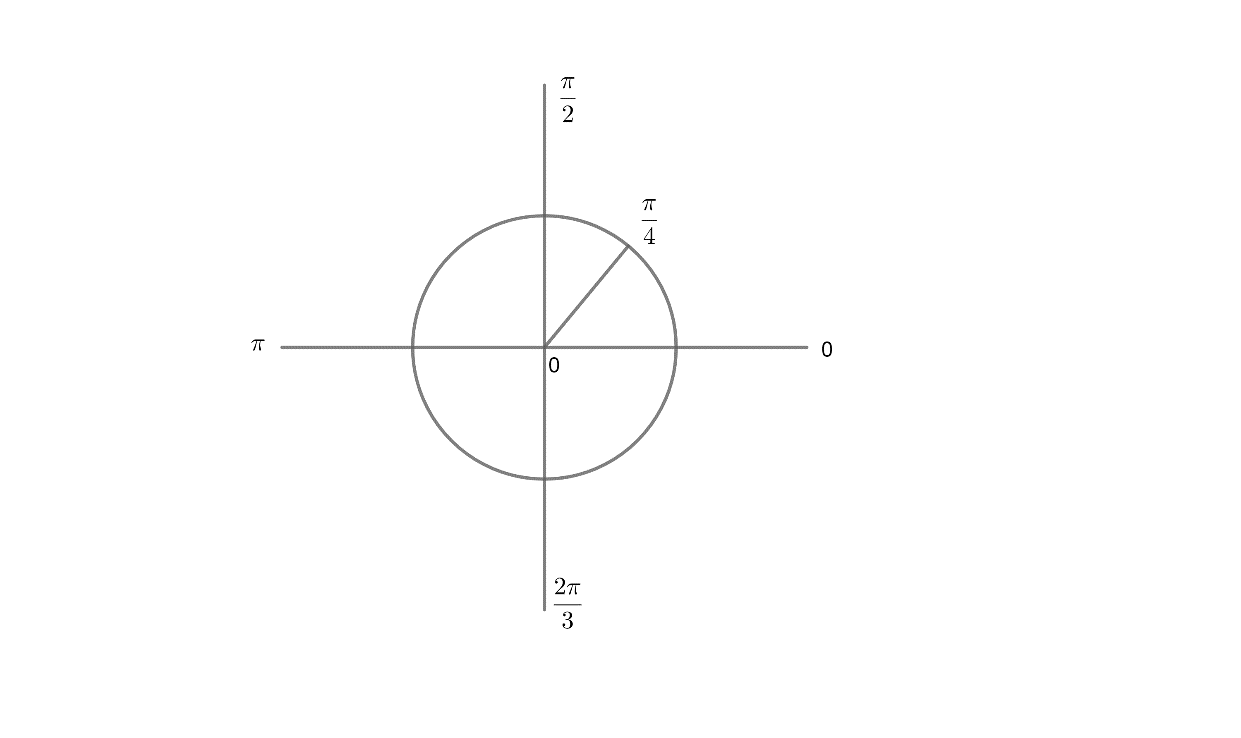
$\cos \theta$
Values
$\cos 0{}^\circ$ =1
$\cos 30{}^\circ$=$\dfrac{\sqrt{3}}{2}$
$\cos 45{}^\circ$=$\dfrac{1}{\sqrt{2}}$
$\cos 60{}^\circ$=$\dfrac{1}{2}$
$\cos 90{}^\circ$=0
$\cos 180{}^\circ$=-1

So, from above we get an idea about the trend of $\cos \theta$ and their values in different angles. Please note that the value of $\cos \theta$ decreases with the increase in angle from the of $\cos \theta$.

In the 1st quadrant $\cos \theta$ is maximum at $\cos 0{}^\circ$ which is the minimum angle possible and value of $\cos 0{}^\circ$ is 1. Also, with the increase in angle the value of $\cos \theta$ decreases.

The value of $\cos 90{}^\circ$ is 0 and the value of $\cos 180{}^\circ$ is -1 which is the minimum value possible for $\cos \theta$.
Also, we know that the value of $\cos \theta$ varies from 1 to -1.

This picture is showing the graph of $\cos \theta$.

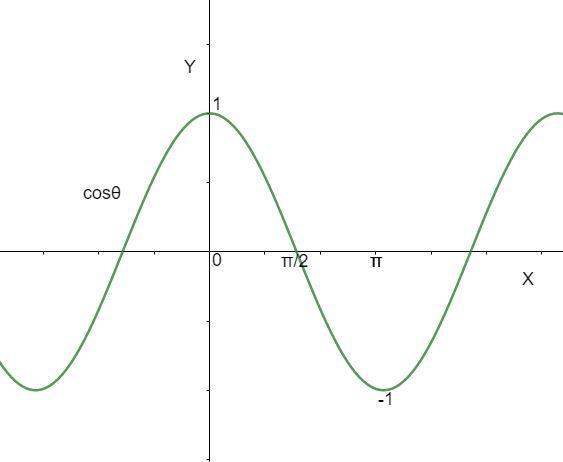
From graph of $\cos \theta$ it is clear that the maximum value of $\cos \theta$ is at $0{}^\circ$which is 1 and the minimum value of $\cos \theta$ is at $180{}^\circ$ which is -1.

Also, we know that if we subtract any greater integer number with any smaller integer number we always get the result as a negative number.

Let us assume that a and b are two positive integer numbers and also a < b.
Then when we subtract (a – b) we get a negative number.

Now, if we analyse the value of $\cos 2{}^\circ$ and $\cos 11{}^\circ$then keeping above discussion in mind we can conclude that the value of $\cos 2{}^\circ$ is greater than the value of $\cos 11{}^\circ$.

As the angle $\cos 2{}^\circ$ is smaller than $\cos 11{}^\circ$. So, it is clear that the value of $\cos 2{}^\circ$is always greater than $\cos 11{}^\circ$. Also, $\cos 2{}^\circ$ and $\cos 11{}^\circ$ both lie in the first quadrant and all the values in the first quadrant are always positive.

So, if we subtract $\cos 2{}^\circ$ from $\cos 11{}^\circ$ then we are subtracting a smaller value from a greater value. So the resulting value is always a negative number and we know that negative numbers are smaller than 0 as they are lying on the left side of 0 in the number line.

This picture is showing a number line of integers.

So, from all the above discussion we can conclude that
$\cos 11{}^\circ -\cos 2{}^\circ <0$
Or, when we subtract $\cos 2{}^\circ$ from $\cos 11{}^\circ$we will get a negative value which is always less than 0 in the first quadrant.

But in question, the statement is $\cos 11{}^\circ -\cos 2{}^\circ >0$ which is incorrect.

Thus, the given statement is false.

Note: This is a basic question and if you know the trend of $\cos \theta$ a different angle then you can even solve this question without writing a single word.

The value of $\cos \theta$ decreases with increase the value of $\theta$.
$\cos \theta$ is maximum at $\cos 0{}^\circ$ and $\cos \theta$ is minimum at $\cos 180{}^\circ$.
$\cos 0{}^\circ =1$ and $\cos 180{}^\circ =-1$

You may directly calculate the value of $\cos 11{}^\circ$ and $\cos 2{}^\circ$ using a calculator.
$\begin{aligned} & \Rightarrow \cos 11{}^\circ -\cos 2{}^\circ <0 \\\ & \Rightarrow 0.98-0.99<0 \\\ & \Rightarrow -0.01<0 \\\ \end{aligned}$

Thus, the given statement in the question is false.