Question

State three characteristics of a series circuit.

Answer 1

Recall that in a series circuit, the path of the circuit usually consists of one single loop with no branches. In this case, think in terms of how the voltage and current would be distributed across each circuit component that acts as a load, and what would be the equivalent resistance of the circuit when they are connected in such a manner. This should help with arriving at a few characteristics of a series circuit.

Formula Used:
Ohm’s law for voltage drop $V =IR$, where I is the current flowing through the resistor, and R is the resistance offered by the resistor.
The net resistance for two resistors $R_1$ and $R_2$ connected in series: $R_{net} = {R_1 +R_2}$

Complete step-by-step solution:
In a circuit, we generally have multiple components connected together. There are two ways in which we can connect two or more components of a circuit, either in series or in parallel.
As the question demands a series circuit, let us deduce what it looks like.
1. A series circuit has all its components connected along a single conductive path.
2. This means that the current flowing through all the components is the same.
3. To have the same current flowing through all components, the voltage dropped by each component (load) will be different and will be dependent on the magnitude of resistance offered by that component. And the sum of all voltage drops across the circuit adds up to the supply voltage of the circuit.
4. Any break in the circuit will render the entire circuit non-functional.
5. The total circuit resistance is equal to the sum of the individual resistance of its components.
As an example, let us look at the following circuit and verify each of the points we have mentioned.

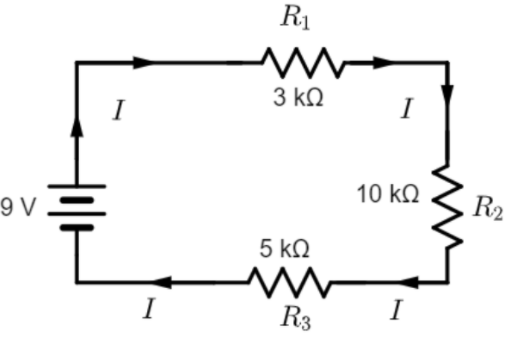
We have a circuit with a 9V battery and three resistances in series since they are all connected across a single conductive path.
The net resistance of the circuit will be the sum of individual resistances:
$R_{net} = R_1 +R_2 + R_3 = 3 +10 +5 = 18\;k\Omega$
Therefore, the current flowing through the circuit will be $I = \dfrac{V}{R_{net}} = \dfrac{9}{18 \times 10^3} = 0.5\;mA$
Let us verify if the sum of voltage drops across the components of the circuit is equal to our supply voltage.
Voltage drop across $R_1$: $V_1 = IR_1 = (0.5 \times 10^{-3})(3 \times 10^3) = 1.5\;V$
Voltage drop across $R_2$: $V_2 = IR_2 = (0.5 \times 10^{-3})(10 \times 10^3) = 5\;V$
Voltage drop across $R_3$: $V_3 = IR_3 = (0.5 \times 10^{-3})(5 \times 10^3) = 2.5\;V$
The sum of voltage drops across individual components:
$= V_1 +V_2 +V_3 = 1.5 +5 +2.5 = 9.0\;V$, which is equal to the supply voltage.
Thus, we have verified the defining characteristics of a series circuit with this circuit.

Note: Remember that when a circuit is connected in series, the current flowing through all circuit components will be the same and the voltage drop across each component may be different, whereas, in a parallel circuit, the voltage across the different branches of the circuit will be the same while the current flowing through the branches gets distributed, with the branch of least resistance getting maximum current flow.