Question

State theorem of parallel axes and theorem of perpendicular axes about the moment of inertia.

Answer 1

To state the above theorem first we need to derive the expression such that it fits the objective of deriving the theorem of parallel axes and perpendicular axes of moment of inertia. The objective of the perpendicular axes theorem is that we have to find the moment of inertia along an axis, perpendicular to the plane for a given moment of inertia along the plane. Similarly the objective of the parallel axes theorem is to find the moment along the axes such that it is parallel to the moment of inertia along the centre of mass.

Complete step by step answer:
To begin with let us first derive the expression for both the theorems as that is how we will be in a position to state the theorems.
Let us first derive the theorem of perpendicular axes of the moment of inertia.
Consider a body in the XY plane as shown in the figure. Let the mass of the body be M. Let us consider only one particle of mass m (denoted by black dot in the figure) lies at a distance y from the x-axes and at a distance x from the y-axes.

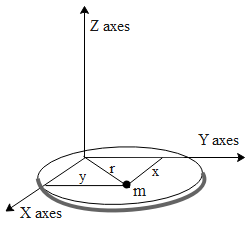
From the above diagram it is clear that ${{r}^{2}}={{x}^{2}}+{{y}^{2}}$.
Let us say we now wish to calculate the moment of inertia along z-axes,
Moment of inertia of the particle about X axes = $m{{y}^{2}}$
Moment of inertia of the body about X axes = ${{I}_{X}}=\sum{m{{y}^{2}}}...(1)$
Moment of inertia of the particle about Y axes = $m{{x}^{2}}$
Moment of inertia of the body about Y axes = ${{I}_{Y}}=\sum{m{{x}^{2}}}...(2)$
The moment of inertia about Z axes is equal to ${{I}_{Z}}=\sum{m{{r}^{2}}}=\sum{m({{x}^{2}}+{{y}^{2}})}$
Hence ${{I}_{Z}}=\sum{m{{x}^{2}}+\sum{m{{y}^{2}}}}$
From equation 1 and 2 we can write the above equation as,
${{I}_{Z}}={{I}_{Y}}+{{I}_{X}}...(3)$
Now let us derive the parallel axis theorem
Let I be the moment of inertia of the body along the axes PQ of mass m. Let RS be the parallel axis through the centre of mass c of the body at a distance d from PQ. Let ${{I}_{CM}}$ be the moment of inertia of the body about the axes RS. Now let us consider a particle of mass M T a distance x from the centre of mass and at a distance (x+d) from PQ.

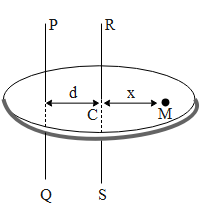
Moment of inertia of the particle about the axis PQ = $M{{(x+d)}^{2}}$. Therefore the moment of inertia of the b entire body about PQ is,
$I={{\sum{M(x+d)}}^{2}}$
$I=\sum{M({{x}^{2}}+{{d}^{2}}+2xd)}$ further we can write this as,
$I=\sum{M{{x}^{2}}+\sum{M{{d}^{2}}}+\sum{M2xd}}$ we know that ${{I}_{CM}}=\sum{M{{x}^{2}}}$ and $\sum{M{{d}^{2}}}=(\sum{M){{d}^{2}}}=m{{d}^{2}}$
The term $\sum{M2xd}=0$since the body can balance itself about its centre of mass and the algebraic sum $\sum{Mx}$ of all the masses is zero.
Hence $I={{I}_{CM}}+m{{d}^{2}}....(4)$
Now using equation 3 and 4 let us state the perpendicular axes and the parallel axes theorem.
Perpendicular axes theorem of moment of inertia: It states that the moment of inertia of a plane lamina about an axis perpendicular to its plane is equal to the sum of moment of inertia of any two mutually perpendicular axis intersecting each other at a point where the perpendicular axis passes through the lamina.
Parallel axes theorem of moment of inertia: it states that moment of inertia of a body about any axis is equal to the moment of inertia to its parallel axis through its centre of mass plus the product of the mass of the body times the square of the distance between the parallel axis.

Note:
It is not mandatory that to state the theorem one has to derive the result. While stating the theorem, towards its end always state the result mathematically. This shows that you have defined the result through mathematics which is generally done.