Question

State the laws of transverse vibrations in stretched strings. Give the procedures for verifying them using a sonometer.

Answer 1

A stretched string, when plucked, produces a transverse wave which travels along the stretched string. These transversal waves reach the end of the strings and are often reflected back. The superposition of the transverse wave with the reflected wave produces a stationary wave.

Complete answer:
We know that the frequency of a wave is given by, $f=\dfrac{v}{\lambda}$ where $v$ is the velocity of the wave and $\lambda$ is the wavelength of the wave. Sonometer is a hollow wooden box, which has a string of length $L$ and mass $m$ is attached to it. This string,then experiences tension $T$. It has a pair of movable bridges which can vary the $L$ of the wire.

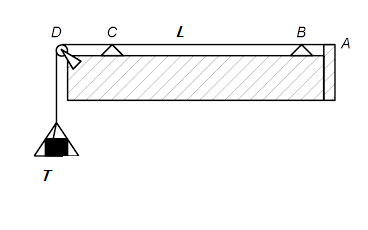
Then the laws of stretched strings gives the relationship between $f$ and the other components of the wave as follows:

1.) The frequency of the wave is inversely proportional to the resonant length $L$ i.e. $f\propto\dfrac{1}{L}$
This can be verified, when a fixed mass $m$ is added to wire , and a small piece of paper is kept on the wire. When a tuning fork of frequency $f_{1}$ is placed on the sonometer, the length of the wire is varied using the bridges. The paper pops up from the wire, when the frequency of the tuning fork $f_{1}$ matches the frequency of the sonometer of length $l_{1}$. Repeat the same for a different $f_{2}$ , then $l_{2}$ is obtained. It is observed that $f_{1}\times l_{1}=f_{2}\times l_{2}=K$ or $f\propto\dfrac{1}{L}$

2.) The frequency of the wave is proportional to square root of the tension $T$experienced by the string i.e. $f\propto\sqrt T$
This can be verified, when the length was kept constant and the weight $m$ is varied measured for different frequencies of the tuning fork. It was observed that the graph of $f$ vs $\sqrt T$ was a straight line. Where $T=mg$

3.) The frequency id the wave is inversely proportional to the square root of the mass per unit length $\mu$ of the string i.e. $f\propto\dfrac{1}{\mu}$

This can be verified, when the length and mass attached to the wire was kept constant, and the experiment was repeated for different materials of wire at different frequencies. It was observed that the graph of $f$ vs $\dfrac{1}{\sqrt \mu}$ was a straight line.
Then, we can say that, $f\propto\dfrac{1}{L}\sqrt{\dfrac{T}{\mu}}$

Note:
Sound waves are also transverse waves. To create a better sounding effect at the theatres and auditoriums, the same principle is used. Thus the walls of the theatres and auditoriums are thick and the ceiling are concave in nature to reflect the sound waves.