Question
Question: State Rolle’s theorem....
State Rolle’s theorem.
Solution
Hint: Rolle’s theorem is a special case of Mean value theorem. So, we will discuss Mean value theorem, then we will state Rolle's theorem with the help of a suitable proof.
Complete step-by-step answer:
It is given in the question to state Rolle’s theorem. So, basically Rolle’s theorem is a special case of Mean value theorem. It can also be called a mean value theorem (MVT). So, (MVT) stated that ‘if f(x) is a function in an interval of (a,b) and f(x) can be differentiable on (a,b) then we have at least one value c in the interval (a,b). Where, a<c<b.
f1(c)=b−af(b)−f(a).
Whereas, Rolle’s theorem is a special case of MVT. Where,
f(a)=f(b). So, here we have f1(c)=0.
f1(c) Rolle’s theorem states that if a function f is continuous on the closed interval [a,b] and differentiable on the open interval (a,b) such that f(a)=f(b). Then f1(c)=0 for some values of c with a≤c≤b.
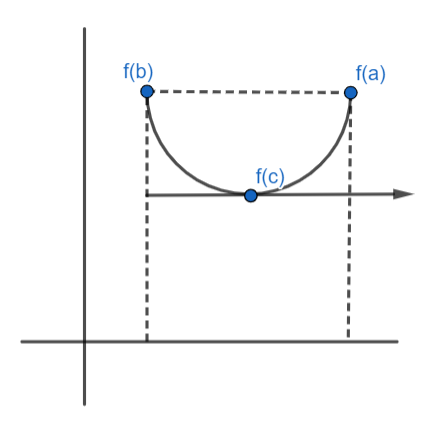
Here in this diagram we have function f(b)=f(a) and f1(c) is parallel to x-axis which means f1(c)=0. So, f is continuous on [a,b]. Therefore, it assumes absolute maximum and minimum values on [a,b].
Note: Rolle’s theorem is important because it gives a necessary condition for critical points; it is used in the proof of the Intermediate value theorem. In fact, IVT is similar to Rolle’s theorem. Rolle’s theorem states that ‘If a function f(x) is defined in the closed interval [a,b] in such a way that it satisfies the following conditions –
1. The function f(x) is continuous in [a,b].
2. f(x) is differentiable in (a,b).
3. f(a)=f(b).
Then there exists at least one value of x such that f1(c)=0’.
