Question

State Right hand thumb rule and fleming's left-hand rule.
The ratio of magnetic moment when two rectangular coils in constant magnetic field B is 4:3 which makes angle $30^\circ {\text{ and 45}}^\circ$ respectively, then find the ratio of the torque produced in the two coils.

Answer 1

The torque produced in a current carrying coil in the presence of magnetic field is given by:
$\tau = (NIA)B\sin \theta$
$or{\text{ }}\tau = MB\sin \theta {\text{ }}\left( {\because {\text{M = NIA}}} \right)$
Where, N is the no. of coils
$I$is the current flowing through it
And A is the area of the coil.
M is the magnetic moment of the coil
B is the strength of magnetic field lines passing through it.
And $\theta$ is the angle between the area vector of coil and magnetic field lines.
Here, in the given question, the magnetic field is constant for both the coils.
Hence, the ratio of the two-torque produced will be given by:
$\dfrac{{{\tau _1}}}{{{\tau _2}}} = \dfrac{{{M_1}{B}\sin 30}}{{{M_2}{B}\sin 45}} = \dfrac{{{M_1}\sin 30}}{{{M_2}\sin 45}}$ and $\dfrac{{{M_1}}}{{{M_2}}} = \dfrac{4}{3}\left( {given} \right)$
Putting the values, we will get the answer.

Complete step by step answer:
Right hand thumb rule: According to the right hand thumb rule, if we imagine holding a current carrying conductor in our right hand so that the thumb points in the direction of current, then the direction in which fingers curl the wire will give the direction of magnetic field lines.

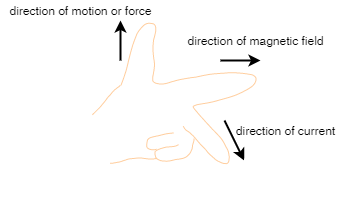
Fleming’s left-hand rule: According to Fleming’s left hand rule, if we stretch our thumb, forefinger and the middle finger of our left hand such that they are mutually perpendicular to each other and if the fore finger points in the direction of magnetic field and the middle finger in the direction of current, then the thumb will point in the direction of motion or force acting on the conductor.

Let us assume rectangular coils, coil 1 and 2 respectively.
In the question it is given that the ratio of the magnetic moments of the coil 1 and 2 is 4:3.
$\Rightarrow {M_1}:{M_2} = 4:3$
It is also given that the direction of the area vector in the two coils makes an angle of $30^\circ {\text{ and 45}}^\circ$ with the magnetic field lines respectively.
The magnetic moment produced in a coil due to current is given by:
$M = NIA{\text{ - - - - - - - - - - - - - - - - - - - - - - - - - - }}\left( 1 \right)$
Where, N is the no. of coils
$I$is the current flowing through it
And A is the area of the coil.
Now, the torque produced in a current carrying coil in the presence of magnetic field is given by:
$\tau = (NIA)B\sin \theta$
$\Rightarrow \tau = MB\sin \theta {\text{ }}\left( {{\text{from}}\left( 1 \right)} \right)$
Where, M is the magnetic moment of the coil
B is the strength of magnetic field lines passing through it.
And $\theta$ is the angle between the area vector of coil and magnetic field lines.
Magnetic field is constant for both the coils.
So, Torque produced in coil 1 is:
${\tau _1} = {M_1}B\sin 30$
Similarly, ${\tau _2} = {M_2}B\sin 45$
The ratio of two torque produced will be:
$\dfrac{{{\tau _1}}}{{{\tau _2}}} = \dfrac{{{M_1}{B}\sin 30}}{{{M_2}{B}\sin 45}} = \dfrac{{{M_1}}}{{{M_2}}}\dfrac{{\dfrac{1}{2}}}{{\dfrac{1}{{\sqrt 2 }}}} \\\ \Rightarrow \dfrac{{{\tau _1}}}{{{\tau _2}}} = \dfrac{4}{3} \times \dfrac{{\sqrt 2 }}{2} = \dfrac{{2\sqrt 2 }}{3} \\\ \Rightarrow {\tau _1}:{\tau _2} = 2\sqrt 2 :3 \\\$

Note:
The general formula for torque produced in a current carrying coil in the presence of magnetic field is given by:
$\tau = \overrightarrow M \times \overrightarrow B \\\ \Rightarrow \tau = MB\sin \theta \\\$
If M and B are constant then,
So, it is maximum when,
$\sin \theta = 1 \\\ \Rightarrow \theta = 90^\circ \\\$
It means if the area vector of the coil is perpendicular to the magnetic field (coil is in the plane of magnetic field) then torque would be maximum.
And torque is minimum when:
$\sin \theta = 0 \\\ \Rightarrow \theta = 0^\circ \\\$
It means if the area vector of the coil is parallel to the magnetic field (coil is in perpendicular plane to magnetic field) then torque would be minimal.