Question

State Kirchhoff’s rule. Use the rules to find the value of ${I_1}$, ${I_2}$ and ${I_3}$.

Answer 1

To solve this question we have used Kirchhoff's laws. As we have to find the current, we need to use that law which has given us a clear idea about the current law and it states that the algebraic sum of currents meeting at a junction is zero.

Formulae used:
$\Sigma I = 0$ and $\Sigma V = 0$ where $\Sigma I$ is the numerical sum of the current and $\Sigma V$ is the sum of energy in a loop.

Complete step by step solution:
Gustav Robert Kirchhoff, a German scientist gave two rules for which deals with the conservation of current and energy in an electrical circuit. These laws are commonly known as Kirchhoff’s rules. The rules are as follows:
The algebraic sum of current at any junction is zero, i.e.,
$\Sigma I = 0$.
The algebraic sum of potential differences across circuit elements of a closed circuit is zero, i.e.,
$\Sigma V = 0$.
By the current rule of Kirchhoff’s;
$\Rightarrow {I_1} + {I_2} + {I_3} = 0$
Applying the 2nd rule in the loop ABCD,
$- 2 - 4{I_1} + 3{I_3} + 1 = 0$
$\Rightarrow 4{I_1} - 3{I_2} = 0$
Again apply 2nd rule in the loop ABFE,
$- 2 - 4{I_1} - 2{I_3} + 4 = 0$

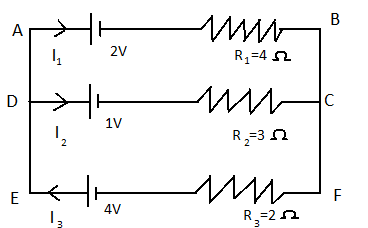
$\Rightarrow 2{I_1} + {I_3} = 0$
Equating the equation obtained from mess ABCD and ABFE with ${I_1} + {I_2} + {I_3} = 0$ ,

We get the values of ${I_1} = \dfrac{2}{3}A$, ${I_2} = \dfrac{7}{{13}}A$ and ${I_3} = \dfrac{9}{{13}}A.$

Additional information: Kirchhoff's laws are used to help us understand how current and voltage work within a circuit. They can also be used to analyze complex circuits that can't be reduced to one equivalent resistance using what you already know about series and parallel resistors. But it works under the assumption that there is no fluctuating magnetic field in the closed loop. Electric fields and emf could be induced which causes the Kirchhoff’s loop rule to break in presence of a variable magnetic field.

Note: While calculating current from kirchoff law it is very important to take care of the direction. In this question, we have taken negative for the current in the direction of the current flow and positive for the reverse direction. We can use the opposite too but remember to apply the same signs in all the loops.