Question

State Kirchhoff’s law of radiation and prove it theoretically.

Answer 1

Hint: Kirchhoff’s law of thermal radiation states that the emissive power to the coefficient of absorption is constant for all the substances at a given temperature. We can say that at a given temperature, the emissivity of a substance is equal to the coefficient of absorption.

Formula used:
$\dfrac{E}{a}=\text{constant =}{{E}_{b}}$

Complete step by step answer:
In heat transfer, Kirchhoff’s thermal radiation law refers to the wavelength-specific radiative emission and absorption by a body in thermodynamic equilibrium. Kirchhoff’s law states that: For a body made up of any arbitrary material, the emitting and the absorbing thermal electromagnetic radiation, the ratio of its emissive power to its coefficient of absorption is equal to a universal function. That universal function describes the emissive power of a perfect black body.
Explanation of Kirchhoff’s thermal radiation law:
If $E$ is the emissive power of a substance and $a$ is the coefficient of absorption, then by Kirchhoff’s law of radiation,
$\dfrac{E}{a}=\text{constant =}{{E}_{b}}$
Or we can say,$a=e$
Theoretical proof of Kirchhoff’s law of thermal radiation:
We will consider two bodies A and B being suspended in a constant temperature enclosure. A is a normal material body and B is a perfectly black body. After some interval of time both A and B will attain the same temperature as that of the enclosure. Prevost heat exchange theory states that every body will emit and absorb thermal radiations.

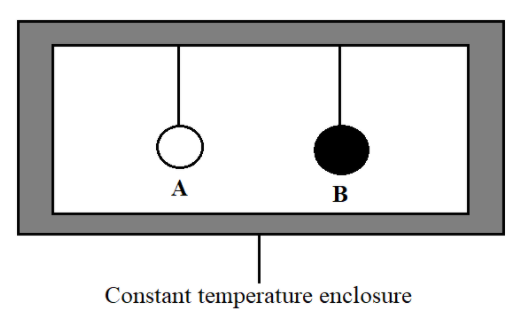
Let $E$ be the emissive power of A and $a$ be its coefficient of absorption. Let ${{E}_{b}}$ be the emissive power of B. Let $Q$ be the radiant heat incident per unit time area of each body.
Heat absorbed by body A per unit time per unit area = $aQ$
Heat emitted by body A per unit time per unit area = $E$
As the temperature remains constant, heat absorbed will be equal to the heat emitted
$E=aQ$
Perfectly black body will absorb the entire heat incident on it
Heat absorbed by body B per unit time per unit area = $Q$
Heat emitted by body B per unit time per unit area = ${{E}_{b}}$
As the temperature remains constant, heat absorbed will be equal to the heat emitted
${{E}_{b}}=Q$
From above equations, we get
$\begin{aligned} & \dfrac{E}{{{E}_{b}}}=\dfrac{aQ}{Q} \\\ & \dfrac{E}{{{E}_{b}}}=a \\\ \end{aligned}$
But, $\dfrac{E}{{{E}_{b}}}=e=\text{coefficient of emission }$
Therefore, $a=e$
Thus, the coefficient of emission is equal to the coefficient of absorption. This proves Kirchhoff’s thermal radiation law theoretically.

Note: Students should keep in mind that Emissivity is a measure of how strongly a body interacts with thermal radiation. Always remember, a high emissivity of material comes together with a high absorptance. Emissivity of a black body is 1.