Question

State Kirchhoff’s law for an electrical network. Using these laws deduce the condition for a balanced Wheatstone bridge. Three resistors $2\Omega ,4\Omega \& 5\Omega$ are combined in parallel. What is the total resistance of the combination?

Answer 1

The Kirchhoff’s law gives the relationship of voltage between two junctions of a circuit as well the current flowing through the circuit. In a balanced Wheatstone bridge, the current flowing across the galvanometer is zero. When resistors are connected in parallel, the voltage across them remains constant.

Complete step by step solution:

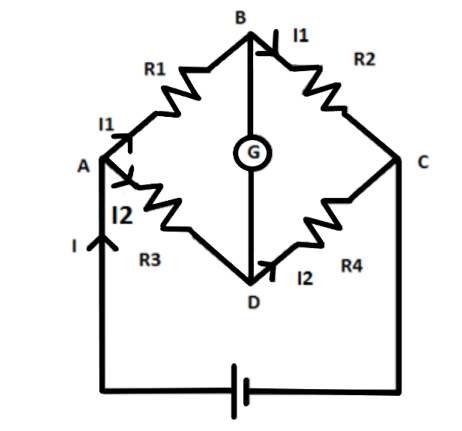
Kirchhoff’s law shows the relationship between the voltages at different points in the circuit. It also describes how the current flows through a circuit.
The two Kirchhoff’s laws are as follows:
1. Loop Law- The summation of the drop of voltage across each component of a circuit is equal to the voltage supplied by the source.
2. Junction Law- The net current; that is incoming and outgoing at each junction should always be zero.
In case of a Wheatstone bridge as shown above, the current flowing across the galvanometer is zero.
Now, using the Ohm’s law which we already know, and applying the loop law for the loop ABDA, we get
$- {I_1}{R_1} + {I_2}{R_3} = 0$
$\dfrac{{{I_1}}}{{{I_2}}} = \dfrac{{{R_1}}}{{{R_3}}}$
For the loop BCDB,
$- {I_2}{R_4} + {I_1}{R_2} = 0$
$\dfrac{{{I_2}}}{{{I_1}}} = \dfrac{{{R_4}}}{{{R_2}}}$
Thus, comparing the two equations, we get
$\dfrac{{{R_1}}}{{{R_3}}} = \dfrac{{{R_4}}}{{{R_2}}}$
Now, the three resistors are connected in parallel, thus the voltage across tem will be constant. Thus the equivalent resistance for the three resistors $R_1$,$R_2$ and $R_3$ that is = $2\Omega ,4\Omega \& 5\Omega$ respectively is R, such that;
$\dfrac{1}{R}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}+\dfrac{1}{{{R}_{3}}}$
$\dfrac{1}{R}=\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{5}$
$R=\dfrac{20}{19}=1.05\Omega$

Note:
When the resistances are connected in parallel, the voltage remains constant and the net resistance is lower than the smallest resistance of the network, while when they are connected in series, the current remains constant and the net resistance is higher than the largest resistance of the network.