Question

State Gauss theorem and use it to derive the Coulomb’s inverse square law.

Answer 1

The gauss theorem is related to the flux due to an electric field. It says that the electric flux coming out of a closed region due to a certain amount of charge within it is directly related to the total amount of charge contained in that closed region.

Complete answer:
A stationary charge produces electric field. The amount of electric field lines passing through a given area is defined as the electric flux. The Gauss theorem relates the electric flux coming out of a closed region due to a certain amount of charge to the total amount of charge contained in that closed region.
The Gauss theorem states that the electric flux through a closed surface is equal to $\dfrac{1}{{{ \in _0}}}$ times the total amount of charge contained in the region. The mathematical expression for Gauss theorem is given as
$\oint {\overrightarrow E .\overrightarrow {dS} } = \dfrac{{{Q_{net}}}}{{{ \in _0}}}$
Here E signifies the electric field passing through a certain area dS. ${Q_{net}}$ is the total amount of charge and ${ \in _0}$ signifies the permittivity of the vacuum.

Derivation of Coulomb’s inverse square law:
Consider a charge +q in place at origin in a vacuum. We want to calculate the electric field due to this charge at a distance r from the charge. Imagine that the charge is surrounded by an imaginary sphere of radius r as shown in the figure below. This sphere is called the Gaussian sphere.

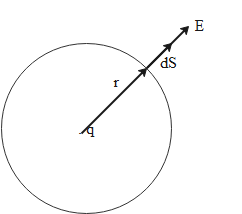
Consider a small area element dS on the Gaussian sphere. We can calculate the flux through this area element due to charge as follows:
$\oint {\overrightarrow E .\overrightarrow {dS} } = \int {EdS\cos 0^\circ }$ (Since angle between electric field and area element is 0$^\circ$)
The electric field due to the charge is constant and we can integrate the area element as follows:

$\oint {\overrightarrow E .\overrightarrow {dS} } = E\int {dS} \\\ = E\left( {4\pi {r^2}} \right) \\\$

Using this in Gauss theorem we get

$E\left( {4\pi {r^2}} \right) = \dfrac{q}{{{ \in _0}}} \\\ \Rightarrow E = \dfrac{q}{{4\pi { \in _0}{r^2}}} \\\$
This is the required Coulomb’s law obtained from Gauss theorem.

Note:
1. If the medium is other than vacuum then the permittivity of the vacuum is replaced by permittivity of that medium in the expression for Gauss theorem.
2. Every problem where Gauss theorem is used, we need a closed Gaussian surface for calculating the electric field.