Question

State Gauss's law. Using this, find an expression for the electric field due to an infinitely long straight charged wire uniform charge density.

Answer 1

- Hint: You can start by defining the Gauss’ law. Then consider an infinitely long charged wire with uniform charge density. Then imagine a cylindrical Gaussian surface and calculate the electric field on the surface of this Gaussian surface by using Gauss’s law equation $\oint\limits_S \phi = \oint\limits_S {\vec E.d\vec s}$

Complete step-by-step solution -
The Gauss’s law states that flux passing through any closed surface is directly proportional to the net charge enclosed in the surface.
Or
This law states that the total flux passing through a surface is equal to $\dfrac{1}{{{\varepsilon _0}}}$times the total charge present on the surface.
Gaussian surface is a closed imaginary surface.

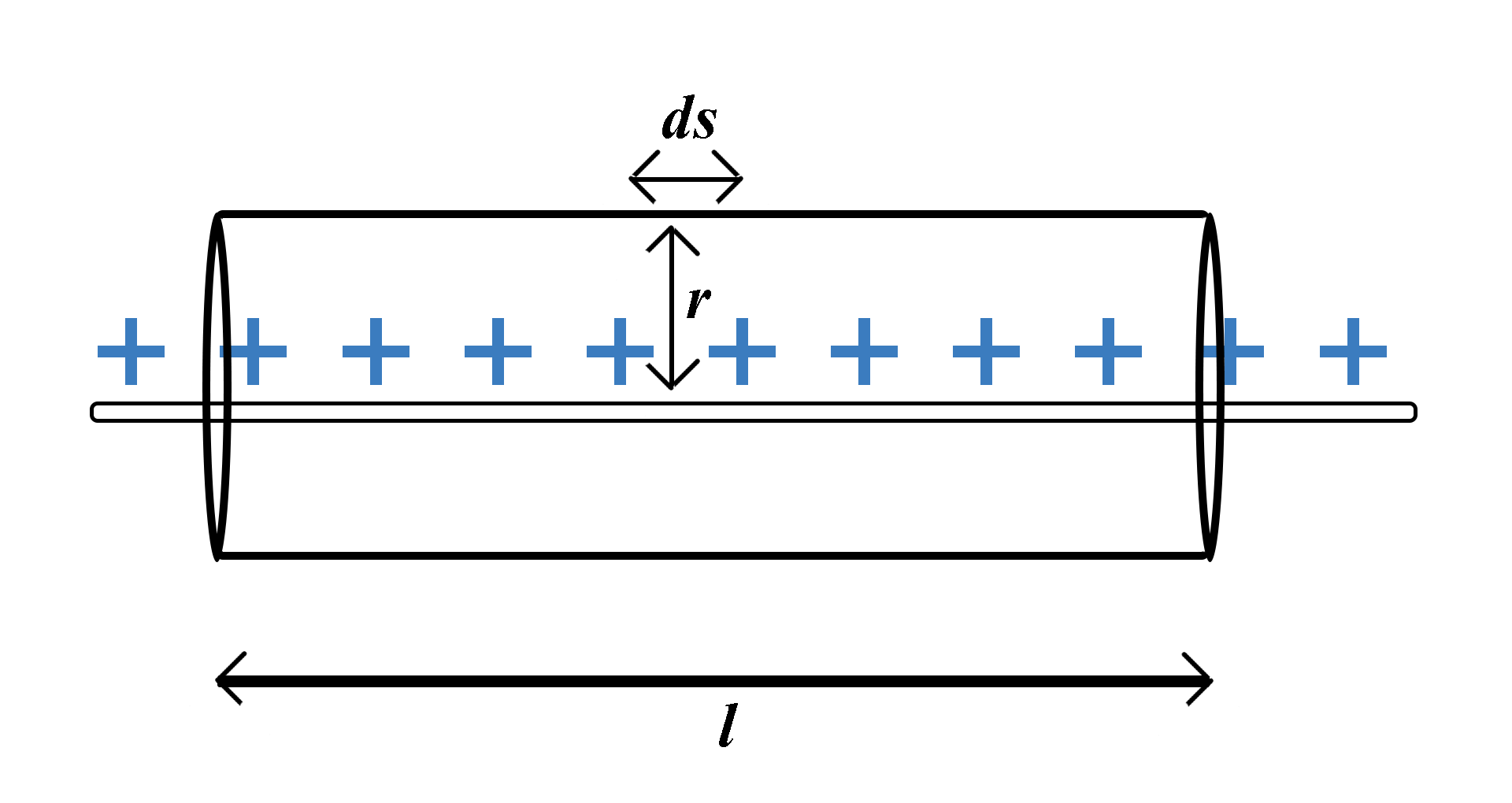
Electric field due to an infinitely long straight wire carrying a charge on it:
Consider an infinitely long current carrying wire. Imagine a point $P$ at some distance $r$from the wire. Now imagine a cylindrical Gaussian surface of length $l$ that has a point $P$ on its surface. So the radius of cylinder is $r$
So, the electric field due to the wire on any point on the surface of the cylinder is the same as every point is equally distant from the wire.
Also for a cylindrical surface the angle that the direction of the electric field makes with the normal will be $0^\circ$.
Consider a very small area $ds$on the surface of the cylinder.
Using Gaussian law on closed curved surface of the cylinder, we get
$\oint\limits_S \phi = \oint\limits_S {\vec E.d\vec s} = \oint\limits_S {\vec E.\hat nd\vec s} = \oint\limits_S {E(1)\cos 0^\circ ds}$
$\Rightarrow \oint\limits_S \phi = E\oint\limits_S {ds}$
$\Rightarrow \phi = E(2\pi rl)$ (Equation 1) $(\because Area{\text{ }}of{\text{ }}the{\text{ }}curved{\text{ }}surface = 2\pi rl)$
For the ends of the cylinder$\theta = 90^\circ$
So$\oint\limits_S \phi = \oint\limits_S {\vec E.d\vec s} = \oint\limits_S {\vec E.\hat nd\vec s} = \oint\limits_S {E(1)\cos 90^\circ ds}$
$\Rightarrow \oint\limits_S \phi = 0$

Consider the charge on the wire enclosed in the cylinder is $q$.
So the linear charge density $(\lambda )$ becomes
$\lambda = \dfrac{q}{l}$
$\Rightarrow q = \lambda l$ (Equation 2)
Also according to Gauss’s theorem
${\phi _E} = \dfrac{q}{{{\varepsilon _0}}}$
$\Rightarrow {\phi _E} = \dfrac{{\lambda l}}{{{\varepsilon _0}}}$(From equation 2)
Now substituting this value of ${\phi _E}$in equation1, we get
$\Rightarrow \dfrac{{\lambda l}}{{{\varepsilon _0}}} = 2E\pi rl$
$\Rightarrow E = \dfrac{\lambda }{{2{\varepsilon _0}\pi r}}$
The equation for the electric field created by an infinitely long charged wire is $E = \dfrac{\lambda }{{2{\varepsilon _0}\pi r}}$.

Note: Always remember that a Gaussian surface is an imaginary surface and the shape of this surface can change from case to case. Like in this solution we considered it as a cylinder for an infinitely long straight wire, for a spherical body we assume a spherical Gaussian surface and for a charged sheet we assume a cylindrical surface.