Question

State Gauss’ Law in electrostatics. Using the law, derive an expression for the electric field due to a uniformly charged thin spherical shell at a point outside the shell.

Answer 1

Hint: Gauss’ Law in electrostatics relates the electric flux passing through a closed surface with the charge enclosed inside it. This law is very useful for deriving the electric field due to various charged bodies of different shapes. We can derive the electric field due to a uniformly thin charged spherical shell at a point outside it by drawing a closed Gaussian surface passing through this point.

Formula used:
$E\oint{dS=}\dfrac{{{Q}_{enclosed}}}{{{\varepsilon }_{0}}}$
$S=4\pi {{R}^{2}}$

Complete step-by-step solution -
Gauss’ law in electrostatics states that the electric flux passing through a closed surface is equal to the ratio of the charge enclosed by the surface to the permittivity of the medium.
Hence, mathematically,
$\phi =\dfrac{{{Q}_{enclosed}}}{\varepsilon }$ --(1)
where $\phi$ is the flux passing through a closed surface enclosing a charge ${{Q}_{enclosed}}$ and $\varepsilon$ is the permittivity of the medium. For vacuum (or air) $\varepsilon ={{\varepsilon }_{0}}$.
The flux $\phi$ through a closed surface can also be written as
$\phi =E\oint{dS}$ --(2)
Where $E$ is the electric field through the surface and $\oint{dS}$ is the total surface area of the closed surface.
Putting (2) in (1), we get,
$E\oint{dS=\dfrac{{{Q}_{enclosed}}}{\varepsilon }}$ --(3)
To derive the electric field due to a uniformly charged thin spherical shell at a point outside the shell, we will use Gauss’ Law. Hence, let us proceed to do that.
Let us take a uniformly charged thin spherical shell of radius $R$ having charge $Q$ uniformly spread on its outer surface.
We will draw a closed Gaussian surface in the form of a circle which is concentric with the spherical shell and has a radius $r$.

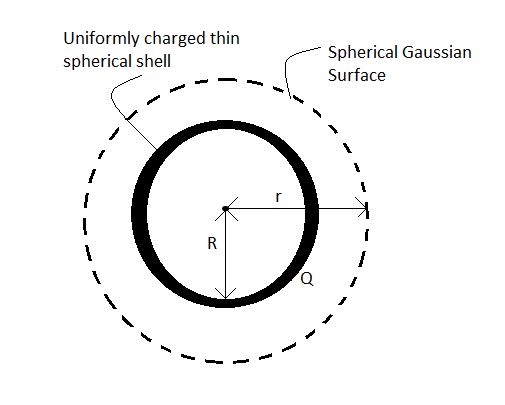
To get the electric field $E$ due to the uniformly charged spherical shell at a distance $r$ from its centre, we will apply Gauss’ law on the spherical Gaussian surface.
Hence, using (3), we get,
$E\oint{dS=\dfrac{{{Q}_{enclosed}}}{\varepsilon }}$ --(4)
Now, for a spherical surface of radius $r$, the surface area $S=\oint{dS}$ is given by
$S=\oint{dS=4\pi {{r}^{2}}}$ --(5)
Also, the charge enclosed in the Gaussian surface in this case is nothing but the total charge on the uniformly charged thin spherical shell. Therefore,
${{Q}_{enclosed}}=Q$ --(6)
Therefore, using (5) and (6) in (4), we get,
$E\times 4\pi {{r}^{2}}=\dfrac{Q}{\varepsilon }$
$\therefore E=\dfrac{1}{4\pi \varepsilon }\dfrac{Q}{{{r}^{2}}}$
Hence, we have derived the electric field at a point outside a uniformly charged thin spherical shell.

Note: Students must remember that the electric field inside the uniformly charged thin spherical is zero. This is because if we draw a Gaussian surface inside the shell, there will be no charge enclosed inside it and hence, from Gauss’ law, the electric field inside it will also be zero. Hence, this also proves the fact that if a charge is given to a thin spherical shell, all of the charge will come out and spread uniformly on the outer surface of the shell.