Question

State Brewster’s law of polarisation of light. The polarising angle for a transparent medium is ${60^ \circ }$. What will be the refractive index and angle of refraction of the medium?
$\tan {60^ \circ } = \sqrt 3$

Answer 1

Hint : Brewster’s law gives the relation between the angle of incidence of an unpolarised light falling on a transparent surface and the refractive index of the reflecting transparent surface.In order to find the refractive index of a medium use Brewster’s law’s mathematical equation and substitute in it the value of angle of incidence. Additionally, find the angle of refraction by subtracting the angle of incidence from the right angle.
Formula Used:
Mathematical expression of Brewster’s law:
$\mu = \tan {i_p}$
where $\mu$is the refractive index of the transparent medium
and ${i_p}$is the angle of incidence of unpolarised light.
Complete step by step answer:
It was discovered by French physicist, Malus that when ordinary light is incident on the surface of a transparent medium, the reflected light is partially plane polarised. And the extent of this polarisation depends on the angle of incidence. There exists a particular angle of incidence such that the reflected light due to it is completely polarised with its vibrations perpendicular to the plane of incidence.
The angle of incidence at which a beam of unpolarised light falling on a transparent surface is completely plane polarised light is called polarising or Brewster angle. It is denoted by ${i_p}$.
Suppose ${i_p}$ is the polarising angle of incidence and ${r_p}$, the corresponding angle of refraction.

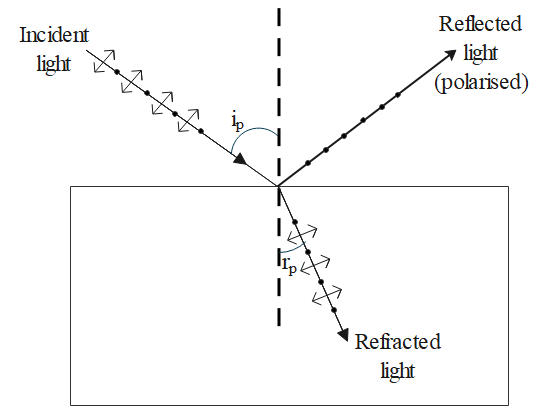
Then
${i_p} + {r_p} = {90^ \circ }{\text{ or }}{{\text{r}}_p} = {90^ \circ } - {i_p}$
From Snell’s law, the refractive index of the transparent medium is:
\eqalign{ & \mu = \dfrac{{\sin {i_p}}}{{\sin {r_p}}} = \dfrac{{\sin {i_p}}}{{\sin \left( {{{90}^ \circ } - {i_p}} \right)}} \cr & \mu = \dfrac{{\sin {i_p}}}{{\cos {i_p}}} \cr & \therefore \mu = \tan {i_p} \cr}
This relation is known as the Brewster’s law. The tangent of the polarising angle of incidence of a transparent medium is equal to its refractive index is the statement of Brewster’s law.
Given:
The polarising angle for a transparent medium,${i_p} = {60^ \circ }$
Refractive index of the transparent medium is given by:
\eqalign{ & \mu = \tan {i_p} \cr & \Rightarrow \mu = \tan {60^ \circ } \cr & \therefore \mu = \sqrt 3 \cr}
Now, angle of refraction is given by:
\eqalign{ & {r_p} = {90^ \circ } - {i_p} \cr & \Rightarrow {r_p} = {90^ \circ } - {60^ \circ } \cr & \therefore {r_p} = {30^ \circ } \cr}

Therefore, the refractive index and angle of refraction of the medium is $\mu = \sqrt 3 {\text{ and }}{r_p} = {30^ \circ }$ respectively.

Note : Another method to solve the same problem is to first calculate the angle of refraction of the medium by subtracting the angle of incidence from the right angle. Later use the value of angle of refraction and angle of incidence to find the value of the refractive index of the transparent medium by taking the sine of these two and then their ratio. Students must avoid making errors in substitution of trigonometric functions’ values.