Question

State Biot-Savart’s law. Define the unit of current.

Answer 1

Recall that the Biot-Savart law relates current flowing through a conductor and the magnetic field produced by it. Try to deduce all the factors that this magnetic field produced may depend on by using Coulomb’s law of electrostatics as an analogy. It would be recommended to analyze this on an elementary level in terms of current elements and length elements taken from a long conductor. Once this is done and you obtain a relation for the magnetic field produced, equate all the parameters to 1 in such a way that you are only left with the current. This would finally help you to define an ampere, which is the unit of current.

Formula Used:
Biot-Savart’s Law for a current element in a current-carrying conductor:
$|dB|= \dfrac{\mu_0}{4 \pi}\left(\dfrac{Idl\;sin\theta}{r^2}\right)$
Where, $dB$ is the magnetic field produced by the current element $dl$, $\mu_0$ is the magnetic permeability, ‘i’ is the current flowing through current element $dl$ and $\theta$ is the angle between $dl$ and r which is the distance of the point from the current element.

Complete step-by-step solution:
Let us begin by understanding the Biot-Savart’s law.
The Biot- Savart law is an equation that describes the magnetic field produced due to a current-carrying segment. This segment is a vector quantity and we call it the current element. This law attributes that any current element projects a magnetic field into the space around it. It is given as:
$|dB|= \dfrac{\mu_0}{4 \pi}\left(\dfrac{Idl\;sin\theta}{r^2}\right)$
Where, $\mu_0$ is the magnetic permeability, I is the current flowing through current element $dl$ and $\theta$ is the angle between $dl$ and r which is the distance of the point from the current element.
Let us look at how this is derived and how this can be used to define an ampere.

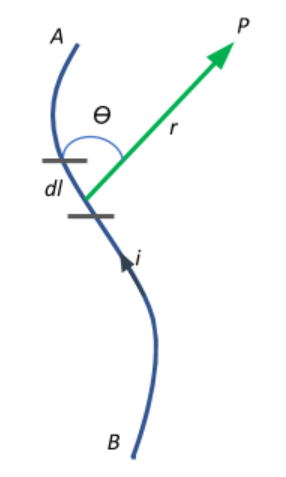
Let AB be a current carrying conductor. Consider a small length element $dl$ of the conductor. Let it carry a current $i$ through its length. This current flowing through the conductor produces a magnetic field all around it, directed in a direction that can be determined by the right hand thumb rule. Let the magnetic field produced by the current element at a point P which is at a distance r be dB. The intensity of the field produced, dB will be
a. Directly proportional to the current flowing through it, $dB \propto i$
b. Directly proportional to the length or the current element of the conductor, $dB \propto dl$
c. Directly proportional to the angle between the conductor and the point, $dB \propto sin\theta$
d. Inversely proportional to the square of the distance between the point P and the current element, $dB \propto \dfrac{1}{r^2}$
Putting all this together we get:
$dB \propto \dfrac{idl\;sin\theta}{r^2} \Rightarrow dB = k\dfrac{idl\;sin\theta}{r^2}$
Where the constant k is determined by the magnetic permeability of the medium between the conductor and the point P. Here, it is air or vacuum, therefore,
$k = \dfrac{\mu_0}{4\pi} = 10^{-7}\; NA^{-2}$
Therefore,
$dB = \dfrac{\mu_0}{4\pi}\dfrac{idl\;sin\theta}{r^2}$
Now, let us consider the current element $dl = 1\;m$, $sin\theta = 1 \Rightarrow \theta = 90^{\circ}$, $r=1\;m$,
$\Rightarrow dB = \dfrac{\mu_0}{4\pi}\dfrac{idl\;sin\theta}{r^2} = 10^{-7}\times i$
Now, if $dB = 10^{-7}\;Wbm^{-1}, then\;i =1A$
Hence, we can define 1A or one ampere as the amount of current that produces a field of $10^{-7}\;Wbm^{-2}$ around a conductor of length 1m that acts on a point that is at a distance of 1m.

Note: Notice that the Biot-Savart’s law in magnetism is similar to Coulomb's law in electrostatics. According to Biot-Savart’s law, the magnetic field $B = \dfrac{\mu_0 I\;dl\;sin\theta}{4\pi r^2}$ is analogous to the electric field $F = \dfrac{q_1 q_2}{4 \pi \epsilon_0 r^2}$.
Also remember that Biot-Savart Law is applicable only for symmetrical current distributions, and to apply it to other systems would mean that even the current would be subjected to a mathematical evaluation.