Question

State Biot-Savart law, giving the mathematical expression for it.
Use this law to derive the expression for the magnetic field due to a circular coil carrying current at a point along its axis.

Answer 1

The Biot-Savart’s law relates the magnetic field produced by a current carrying element at a point with the magnitude of the current, length of the element, and the distance of the point from the element. Considering an element of a circular coil, we can write the magnetic field produced by it at the given point and integrate it to get the total magnetic field.

Complete step-by-step solution:
Let there be a conductor carrying a current of $I$. Consider an infinitesimal length $dl$ of this conductor. The magnetic field due to this small element at the point P located at a distance of $r$ from it is to be obtained. According to the Biot-Savart law, the magnetic field is proportional to the length $dl$, the current $I$ and inversely proportional to the square of the distance of the point $r$ from the element. Also, its direction is perpendicular to the plane formed by $dl$ and $r$. So in vector form, the above proportionality can be expressed as
d\vec B \propto \dfrac{{Id\vec l \times \overset{\lower0.5em\hbox{\smash{\scriptscriptstyle\frown}}}{r} }}{{{r^2}}}
\Rightarrow d\vec B = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{Id\vec l \times \overset{\lower0.5em\hbox{\smash{\scriptscriptstyle\frown}}}{r} }}{{{r^2}}}
Here $\dfrac{{{\mu _0}}}{{4\pi }}$is the proportionality constant.
Let us consider a circular coil of radius $R$ carrying a current $I$, in the y-z plane. We consider a point P at a distance $x$ from the centre of the coil along the x-axis.

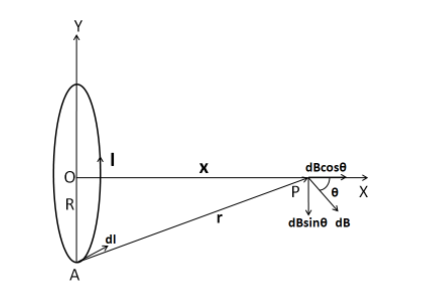
The magnetic field at the point P due to an infinitesimally small element of length $dl$ is given by
d\vec B = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{Id\vec l \times \overset{\lower0.5em\hbox{\smash{\scriptscriptstyle\frown}}}{r} }}{{{r^2}}}..............(1)
Since the plane of the coil is along the Y-Z plane, so $d\vec l$ is perpendicular to \overset{\lower0.5em\hbox{\smash{\scriptscriptstyle\frown}}}{r} so that we have \left| {d\vec l \times \overset{\lower0.5em\hbox{\smash{\scriptscriptstyle\frown}}}{r} } \right| = dl
Putting this in (1) we get
$dB = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{Idl}}{{{r^2}}}$........................(2)
In the triangle OAP applying the Pythagoras theorem we have
$A{P^2} = O{A^2} + O{P^2}$
$\Rightarrow {r^2} = {R^2} + {x^2}$.......................................(3)
Putting (3) in (2) we have
$dB = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{Idl}}{{\left( {{R^2} + {x^2}} \right)}}$......................(4)
The direction of $d\vec B$ is as shown in the above figure. Now, we have considered the horizontal and the vertical components of $d\vec B$ in the above figure. The vertical components of all such elements will get cancelled with each other. But the horizontal components will get added. The horizontal component is given by
$d{B_H} = dB\cos {\theta}$
From (4)
$d{B_H} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{Idl}}{{\left( {{R^2} + {x^2}} \right)}}\cos {\theta}$ ………………...(5)
From the above figure, we have
$\cos {\theta} = \dfrac{R}{{{{\left( {{x^2} + {R^2}} \right)}^{1/2}}}}$
Putting this in (5) we have
$d{B_H} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{Idl}}{{\left( {{R^2} + {x^2}} \right)}}\dfrac{R}{{{{\left( {{x^2} + {R^2}} \right)}^{1/2}}}}$
$\Rightarrow d{B_H} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{RI}}{{{{\left( {{x^2} + {R^2}} \right)}^{3/2}}}}dl$
Integrating both sides, we have
$\int_0^B {d{B_H}} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{RI}}{{{{\left( {{x^2} + {R^2}} \right)}^{3/2}}}}\int_0^{2\pi R} {dl}$
$\Rightarrow B = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{RI}}{{{{\left( {{x^2} + {R^2}} \right)}^{3/2}}}}2\pi R$
On simplifying, we finally get
$B = \dfrac{{{\mu _0}I{R^2}}}{{2{{\left( {{x^2} + {R^2}} \right)}^{3/2}}}}$
Hence, this is the required expression for the magnetic field due to a circular coil carrying current at a point along its axis.

Note: Do not forget to take the components of the magnetic field before integrating. This is because the magnetic field is a vector quantity, and hence we have to add it vectorially.