Question

State and prove the theorem of parallel axes about moment of inertia.

Answer 1

Hint: Parallel axes theorem is used when we want to find the moment of inertia of a body about an axis. However, we must know the moment of inertia about an axis passing through the centre of mass of the body and parallel to the axis about which we find the centre of mass.

Complete step-by-step answer:
Inertia is a property of a body to resist the change in linear state of motion it is measured by the mass of the body. The moment of inertia (I) of a body is a measure of its ability to resist change in its rotational state of motion. Moment of inertia of a particle about a given axis is $I=m{{r}^{2}}$, m is the mass of the particle and r is the perpendicular distance of the particle from the rotational axis. Moment of inertia of a body made up of number of particles about an axis is given by $I={{m}_{1}}r_{1}^{2}{{m}_{2}}r_{2}^{2}+{{m}_{3}}r_{3}^{2}+{{m}_{4}}r_{4}^{2}+.........$ Moment of inertia of a rigid body about an rotational axis is calculated by the treating the body as a continuous distribution of small element of dm mass. Therefore, the moment of inertia (dI) of an element at a distance r from the axis is $dI=dm{{r}^{2}}$. Then, $I=dmr_{1}^{2}+dmr_{2}^{2}+dmr_{3}^{2}+.......=\sum{dmr_{i}^{2}}=\int{dm{{r}^{2}}}$
Suppose we want to find the rotational inertia (I) of a body of mass M about a given axis. We can find it by the integration of $\int{dm{{r}^{2}}}$. However, there is a neat shortcut if we happen to know the rotational inertia (Icom) of the body about a parallel axis that extends through the body’s centre of mass. Let d be the perpendicular distance between the given axis and the through the centre of mass (remember these two axes must be parallel). Then the rotational inertia (I) about the given axis is $I={{I}_{com}}+M{{d}^{2}}$, where M is the total mass of the body. Think of the distance d as being the distance we have shifted rotation axis from the being through the com. This equation is known as the parallel axis theorem. We shall now prove it.
Now, we shall prove the theorem of parallel axes.
Suppose we take an arbitrarily shaped body. We look at it in such a way that the axis of rotation is going inside the page (perpendicular to the plane of the page). Let O be the centre of mass of the body. Place the origin of the coordinates at O. consider an axis through PO perpendicular to the plane of the figure, and another axis through point P parallel to the first axis. Let the x and y coordinates of P be a and b.

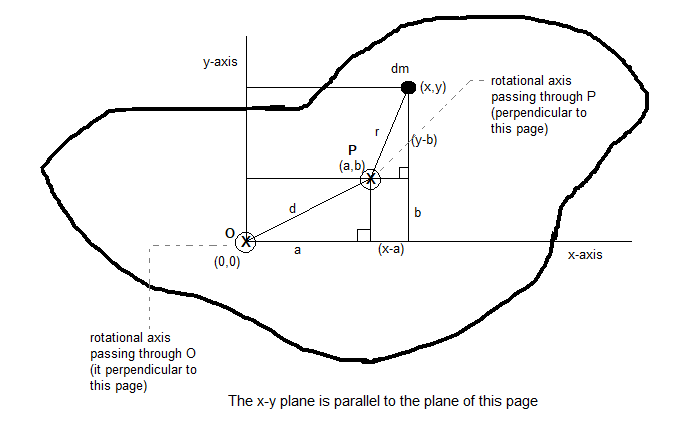
(This figure is a cross section of the body. Think, as you are looking at the body from the top view.)

Let dm be a mass element with the general coordinates x and y. the rotational inertia of the body about the axis through P is $I=\int{dm{{r}^{2}}}=\int{\left[ {{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}} \right]dm}$.
$\Rightarrow I=\int{\left[ {{x}^{2}}-2ax+{{a}^{2}}+{{y}^{2}}-2by+{{b}^{2}} \right]dm}$
Open the bracket and rearrange the terms.
$\Rightarrow I=\int{\left( {{x}^{2}}+{{y}^{2}} \right)dm}+\int{\left( {{a}^{2}}+{{b}^{2}} \right)dm}-2a\int{x}dm-2b\int{y}dm$ …….(i)
From the definition of the centre of mass, the last two integrals in the above equation given the x and y coordinates of the centre of mass and we have taken the position of centre of mass to be the origin. Therefore, the x and y coordinate of centre of mass will be zero implying the two integrals to be equal to zero.
$\int{\left( {{x}^{2}}+{{y}^{2}} \right)dm}$, in this integral, as you can see in the figure ${{x}^{2}}+{{y}^{2}}={{r}^{2}}$ and r is the perpendicular distance of point P from the given axis of rotation passing through the centre of mass. Therefore, $\int{\left( {{x}^{2}}+{{y}^{2}} \right)dm}=\int{{{r}^{2}}dm}$, which is equal to the moment of inertia (Icom) of the body about the axis passing through its centre of mass.
$\int{\left( {{a}^{2}}+{{b}^{2}} \right)dm}$, in this integral, as you can see in the figure ${{a}^{2}}+{{b}^{2}}={{d}^{2}}$ Therefore, $\int{\left( {{a}^{2}}+{{b}^{2}} \right)dm}=\int{{{d}^{2}}dm}$. Since, d is a constant distance; it can be taken outside the integral.
$\int{{{d}^{2}}dm}={{d}^{2}}\int{dm}=M{{d}^{2}}$.
Substitute all the values that we found in equation (i).
After substituting, we will get,
$I={{I}_{com}}+M{{d}^{2}}$. Hence, the theorem is proved.

Note: It is important to remember that to use the parallel axis theorem, both the axes must be parallel to each other and one of the axes must be passing through the centre of mass of the body. Otherwise the theorem is not applicable.