Question

State and prove Pascal’s Law of transmission of fluid pressure.

Answer 1

In this question, the concept of Pascal's law is used, that is it states that if a static pressure is applied from outside of a confined fluid, the pressure is evenly distributed throughout every portion of fluid.

Complete step by step solution:
As we know that Pascal's law states that if a static pressure is applied from outside of a confined fluid, the pressure is evenly distributed throughout every portion of fluid. According to the law, if $F$ is the applied force, $P$is the transmitted pressure, and $A$ is the area of applied pressure then from Pascal’s law relation of these three will be
$\Rightarrow F = P \times A$

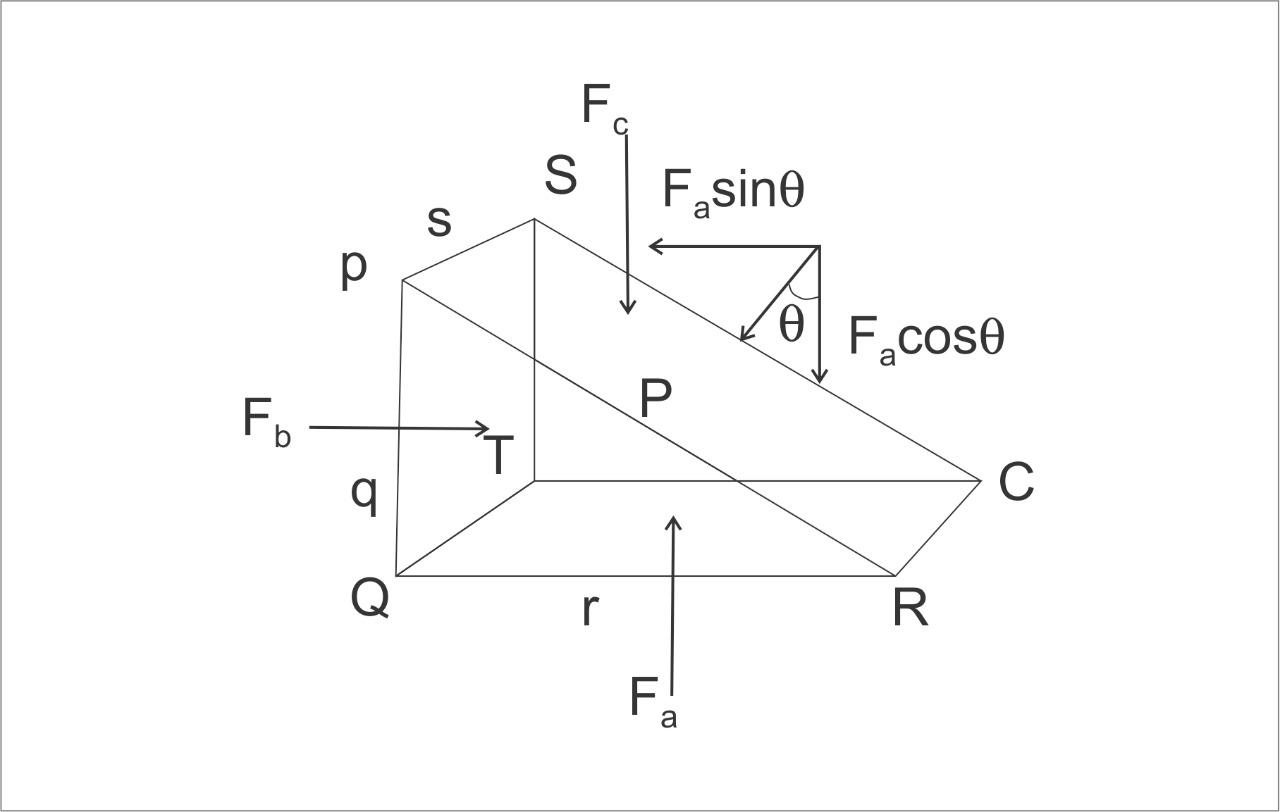
Fig: Pressure and Force distribution in triangular prism

Now, we assume a right angled prismatic triangle containing a fluid of density$\rho$.the prism being very small, we consider every point at the same depth, and gravitational effect on prism is also the same in those points.
Let $ps$, $qs$and $rs$ be the area of surfaces $PSUR$, $PSTQ$ and $TURQ$ of the prism.
And also, pressure on those surfaces be, ${P_b}$ and ${P_c}$ respectively.
A force is exerted by the pressure in surfaces, in $PRUS$ face the force be ${F_a}$, in $PSTQ$ the force be ${F_b}$ and in $TURQ$ the force be ${F_c}$.
Now, we write the expression for the forces at different surfaces as,
$\Rightarrow {F_a} = {P_a} \times ps$
$\Rightarrow {F_b} = {P_b} \times qs$
$\Rightarrow {F_c} = {P_c} \times rs$
As it is right angled triangular prism,
$\Rightarrow \sin \theta = \dfrac{q}{p}$
$\Rightarrow \cos \theta = \dfrac{r}{p}$
As we know that the total force inside the prism will be zero, as equilibrium is attained.
Breaking the ${F_a}$ force into horizontal and vertical directions as ${F_a}\sin \theta$ and ${F_a}\cos \theta$, we get
$\Rightarrow {F_a}\sin \theta = {F_b}......(1)$
$\Rightarrow {F_a}\cos \theta = {F_c}......(2)$
Replacing ${F_a}$ with ${P_a} \times ps$ and the value of ${F_b}$ with ${P_b} \times qs$ putting values of $\sin \theta$ in equation$(1)$
$\Rightarrow {P_a} \times ps \times \dfrac{q}{p} = {P_b} \times qs.....(3)$
Similarly, from equation $(2)$ putting the values we get
$\Rightarrow {P_a} \times ps \times \dfrac{r}{p} = {P_c} \times rs......(4)$
Now, from equation $(3)$ and $(4)$ we get,
${P_a} = {P_b}$ And ${P_a} = {P_c}$
$\therefore {P_a} = {P_b} = {P_c}$

So, the pressure distributed in the fluid is equal in every direction.

Note: As we know that the Pascal Law has wide application for example it is used in the hydraulic press, which is the great achievement of Pascal’s Law application, in modern planes it is used for brakes, landing and various purposes.