Question

State and explain the law used to determine the magnetic field at a point due to a current element. Derive the expression for the magnetic field due to a circular current-carrying loop of the radius $r$ at its center.

Answer 1

Just keep in mind, the magnetic field at a point is calculated using BIOT-SAVART’S law. We will use this law to derive the expression for the magnetic field due to a circular current-carrying loop at the center of a loop having a radius $r$.

Complete step by step solution:
We will define the law used to calculate the magnetic field and then we will derive the expression for the magnetic field due to a current-carrying loop of the radius $r$ at its center.

Now, the law used to determine the magnetic field at any point due to a current-carrying conductor is BIOR-SAVART’S LAW.
Now, let us know what is BIOT-SAVART’S LAW?
For this, consider a small element AB of the length $dl$ of a conductor carrying current $I$.

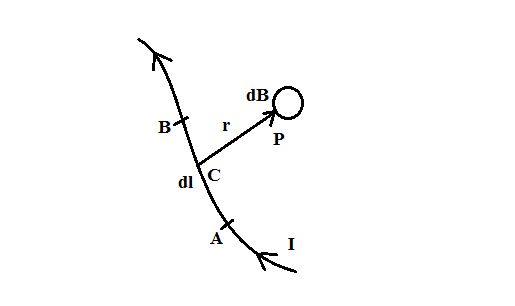
Here, AB is the small element of length $dl$ carrying-current $I$, $dB$ is the strength of the magnetic field. Here, we will consider a point P at a distance $r$ from the element, where we will calculate the magnetic field.
Now, the strength of the magnetic field $dB$ at a point P is found to be depended upon quantities as under:
i) $dB\, \propto \,dl$
ii) $dB\, \propto \,I$
iii) $dB\, \propto \,\sin \theta$, the angle subtended at point C.
iv) $dB\, \propto \,\dfrac{1}{{{r^2}}}$
Combining $(i)$ to $(iv)$, we get
$dB\, \propto \,\dfrac{{I\,dl\,\sin \theta }}{{{r^2}}}$
$\Rightarrow \,dB = k\dfrac{{I\,dl\,\sin \theta }}{{{r^2}}}$
Where, $k$ is the constant of proportionality.
Now, we will derive the magnetic field due to a current-carrying loop.
For this, consider a circular coil or a circular loop of radius $R$, carrying current $I$. The circular coin consists of a large number of current elements each of length $dl$. Consider one such current element (AB) $Id\vec l$ .

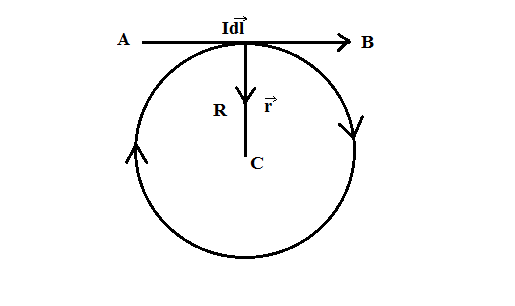
Here, $I$ is the current in the loop. Now, we will consider a point C at a distance $R$ from the small element AB, where the electric field is to be calculated.
Now, we will use BIOT-SAVART’S LAW to calculate the magnetic field at a point C, which is given by
$d\vec B = \dfrac{{{\mu _0}}}{{4\pi }}\,\dfrac{{I\,d\vec l \times \hat r}}{{{R^2}}}$
Since, the angle between $d\vec l$ and $\hat r$ is $90^\circ$. So, $d\vec l \times \hat r = \,dl\,\sin 90^\circ = \,dl$

Therefore, we get,
$dB = \dfrac{{{\mu _0}}}{{4\pi }}\,\dfrac{{I\,dl}}{{{R^2}}}$
Now, the magnetic field at the center can be calculated by integrating the above equation over the closed-loop. Therefore, we get
$\oint {dB = \oint {\dfrac{{{\mu _0}}}{{4\pi }}\,\dfrac{{I\,dl}}{{{R^2}}}} }$
Here, ${\mu _0}$, $I$, $4\pi$ and $R$ are the constants.
$\therefore$ $B = \dfrac{{{\mu _0}}}{{4\pi }}\,\dfrac{1}{{{R^2}}}\,\oint {dl}$
$\Rightarrow$ $B = \dfrac{{{\mu _0}I}}{{4\pi }} \times 2\pi R$ ($\because \,\,\oint {dl = 2\pi R}$)
$\Rightarrow$ $B = (\dfrac{{{\mu _0}}}{{4\pi }})\,\dfrac{{2\pi I}}{R}$

Therefore, from the above relation, we can say that the direction of the magnetic field at the center of the current-carrying loop is perpendicular to the plane and in the downward direction.

Additional Information:
If the coil consist of N turns, then the magnetic field due to the current-carrying coil at its center is given by $B = \dfrac{{{\mu _0}}}{{4\pi }}\,\dfrac{{N \times 2\pi I}}{R}.$

Note: In the above relation, we will see that, the value of $K$ is given by $K = \dfrac{{{\mu _0}}}{{4\pi }}.$
Here, ${\mu _0}$is the absolute permeability of free space. Also, the value of ${\mu _0}$ in $SI$ units is given by ${\mu _0} = 4\pi \times {10^{ - 7}}T\,m\,{A^{^{ - 1}}}$.