Solveeit Logo
Login

Question

Question: Starting from rest, a flat car is given a constant acceleration \({{a}_{o}}=2m/{{s}^{2}}\). A cable ...

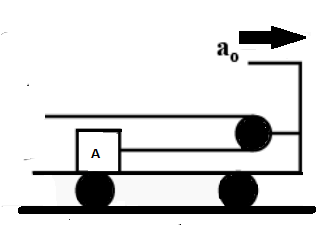
Starting from rest, a flat car is given a constant acceleration ao=2m/s2{{a}_{o}}=2m/{{s}^{2}}. A cable is connected to a crate A of mass 50kg50kg as shown. Neglecting the friction between floor and car wheels and mass of pulley. The coefficient of friction between the crate and floor of the car is μ=0.3\mu =0.3. The tension in the cable is

Explanation

Solution

In order to solve the question we have to consider the concept of equilibrium of force. We should also have to keep in mind that the frictional force is in the opposite direction of the motion. As given in the figure we can clearly see that the wire is going round the pulley and its acceleration will be twice that of the cart (pulley) as the wire does cross over the pulley.
Formula Used: We are going to use the following formula to solve the problem:-
T−f=maT-f=ma.

Complete step-by-step solution
From the question above we have the following parameters with us:-
Acceleration of car, ao=2m/s2{{a}_{o}}=2m/{{s}^{2}}.
Acceleration of the crate a=2×2=4m/s2a=2\times 2=4m/{{s}^{2}} because the wire is going round the pulley and its acceleration will be twice as that of the cart because the wire does cross over the pulley.
Mass of crate A, m=50kgm=50kg
We have to calculate the tension, TT in the cable.
We have the following figure with us:-

The free-body diagram of the block will be as follows:-

From the free body diagram and according to the question normal reaction (NR) and weight (mg) will balance each other.
Therefore, the net force on the block will be given as follows:-
T−f=maT-f=ma………….. (i)(i)where ff is the frictional force on the block.
But, f=μNf=\mu N………………… (ii)(ii)
Equation (ii)(ii) is the formula of frictional force. The frictional force is the product of the coefficient of friction and normal reaction.
Putting (ii)(ii)in (i)(i) we get
T−μN=maT-\mu N=ma……………. (iii)(iii)
Putting the values of the parameters we get
T−50×0.3×10=50×4T-50\times 0.3\times 10=50\times 4 (as N=mgN=mg)
⇒N−150=200\Rightarrow N-150=200
⇒T=200+150\Rightarrow T=200+150
⇒T=350N\Rightarrow T=350N
Therefore the tension in the cable will be, T=350NT=350N

Note: We have to take care of the acceleration of the crate as it is twice that of the car because the wire does cross over the pulley. Drawing a correct free body diagram is a very important aspect of solving these types of problems. We can also take the value of g=9.8ms−2g=9.8m{{s}^{-2}} .