Question

Starting from rest, a car moves with uniform acceleration and attains a velocity of $72Km{{h}^{-1}}$ in $2s$. It then moves with uniform speed for $25s$ and is then brought to rest in $10s$ under uniform retardation. Find the total distance travelled using the velocity time graph.

Answer 1

When a car is travelling at different speeds and with different accelerations for various intervals of time, we can apply the equations of motion and distance speed time relation on the motion of the car between those intervals. After calculating the velocity of the car at different intervals, we will plot a velocity-time graph for the motion of the car, and the area of that graph will give us the total distance travelled by the car during its motion.

Complete step-by-step answer:
First case,
Car has started from rest
At $t=0$
Velocity $u=0$
Second case,
Car moves with uniform acceleration for $2s$ and attains a velocity of $72Km{{h}^{-1}}$
At $t=2s$
$\begin{aligned} & v={{u}_{1}}=72Km{{h}^{-1}}=72\times \dfrac{5}{18}m{{s}^{-1}} \\\ & {{u}_{1}}=20m{{s}^{-1}} \\\ \end{aligned}$
Third case,
Car moves with the same speed for next$25s$
At $t=27s$
$v={{u}_{1}}=20m{{s}^{-1}}$
Fourth case,
Car is brought to rest in next $10s$
At $t=27+10s=37s$
$v=0$
Velocity-time graph for the motion of the car:

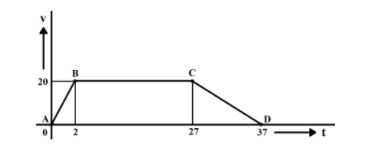
Distance travelled by the car over the motion is given by the area of the velocity-time graph.
The graph obtained is of trapezium shape. For calculating the area of the graph under the curve, we will apply the formula for calculating the area of a trapezium with non-parallel and unequal sides.
Area of trapezium is given as,
$A=\dfrac{1}{2}\left( \text{sum of parallel sides }\times \text{ separation between parallel sides} \right)$
Non parallel sides are marked as BC and AD
From the graph,
Length of BC is $25\text{ units}$
Length of AD is $37\text{ units}$
And,
Separation between parallel sides is $10\text{ units}$
Area of the trapezium,
$A=\dfrac{1}{2}\times \left( 25+37 \right)\times 10=620\text{ units}$
The total distance travelled by the car is $620m$

Note: For calculating the area of the velocity-time graph, we can use the below approach:
The trapezium figure in the graph can be assumed as made of two right-angled triangles and a rectangle. We can find the area of the individual curve using different markings in the graph.

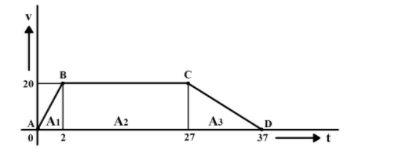
Area of the first triangle,
Length of the base is $2\text{ units}$
Length of the height is $20\text{ units}$
$\begin{aligned} & A=\dfrac{1}{2}\times B\times H \\\ & A=\dfrac{1}{2}\times 2\times 20=20 \\\ & {{A}_{1}}=20\text{ units} \\\ \end{aligned}$
Area of the rectangle,
Length of the rectangle is $25\text{ units}$
Breadth of the rectangle is $20\text{ units}$
$\begin{aligned} & A=L\times B \\\ & A=25\times 20=500 \\\ & {{A}_{2}}=500\text{ units} \\\ \end{aligned}$
Area of the second triangle,
Length of the base is $10\text{ units}$
Length of the height is $20\text{ units}$
$\begin{aligned} & A=\dfrac{1}{2}\times B\times H \\\ & A=\dfrac{1}{2}\times 10\times 20=100 \\\ & {{A}_{3}}=100\text{ units} \\\ \end{aligned}$
Total area is given as,
$\begin{aligned} & A={{A}_{1}}+{{A}_{2}}+{{A}_{3}} \\\ & A=20+500+100=620 \\\ & A=620\text{ units} \\\ \end{aligned}$
The total distance travelled by the car is $620m$