Question

Standing waves are produced in $10m$ long stretched strings. If the string vibrates in 5 segments and wave velocity is $20m{s^{ - 1}}$ , then its frequency will be
A. $5Hz$
B. $2Hz$
C. $10Hz$
D. $12Hz$

Answer 1

To answer the question, we will build a simple diagram based on the question. The entire length of the string is $10m$ , and there are five segments, so we will compute the length of one segment and determine the value of $\lambda$ , and then calculate the frequency $(\nu )$ using this $\lambda$ .

Complete answer:
Before we go into the question, let's have a look at what a standing wave is. The combination of two waves flowing in opposite directions, each with the same amplitude and frequency, is known as a standing wave.
Now, let us come to the question;
The wavelength of a stretched string's fundamental vibrational mode is twice the length of the string.

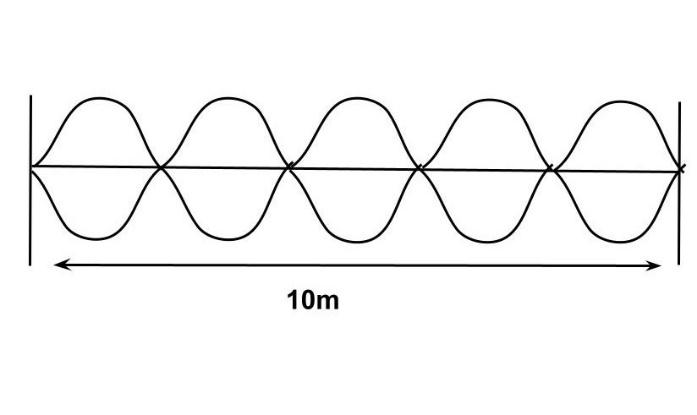
Because the string produces standing waves and vibrates in five parts, it can be shown as
$\therefore 5\dfrac{\lambda }{2} = 10$
Therefore, from here we will find value of $\lambda$
$\Rightarrow \lambda = 4{\mkern 1mu} m$
The wave's velocity, $v$ , is given to us in the question as $v = 20m{s^{ - 1}}$
Hence, the frequency will be $\nu = \dfrac{v}{\lambda } = \dfrac{{20}}{4} = 5{\mkern 1mu} {s^{ - 1}} = 5{\mkern 1mu} Hz$
Therefore, the frequency is $5Hz$
The correct option is: (A) $5Hz$

Note:
It's important to note that standing waves don't just appear out of nowhere. They call for energy to be delivered into a system at a specific frequency. That is, when a system's driving frequency is identical to its natural frequency. Resonance is the term for this situation. Standing waves are invariably linked to resonance.