Question
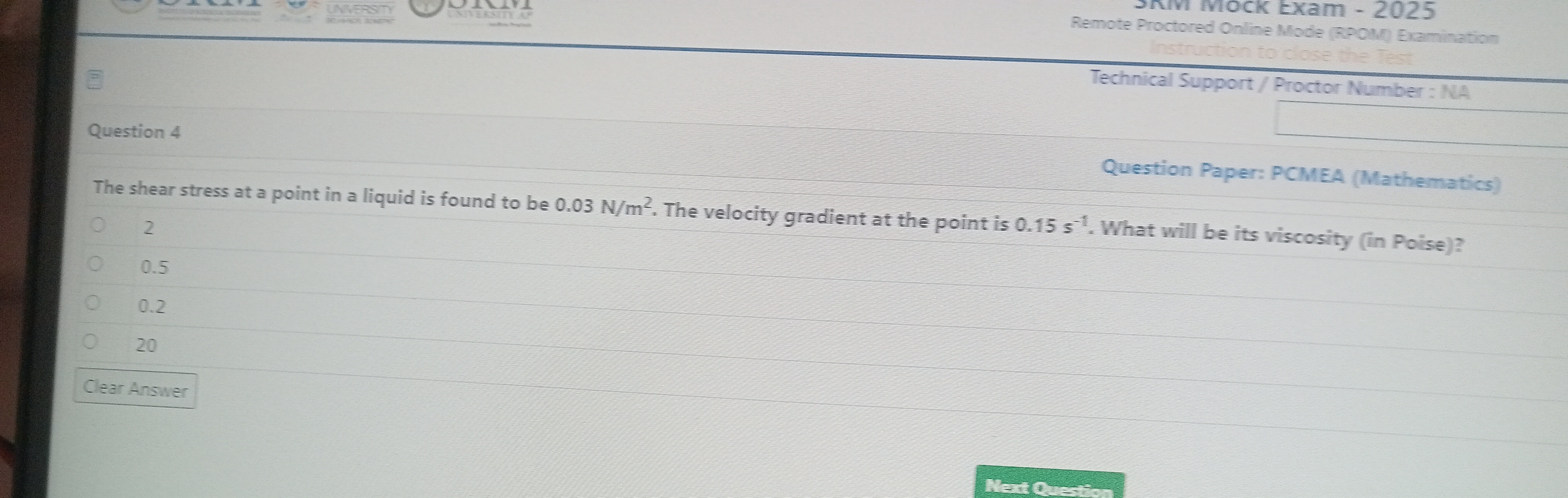
Question: The shear stress at a point in a liquid is found to be 0.03 N/m². The velocity gradient at the point...
The shear stress at a point in a liquid is found to be 0.03 N/m². The velocity gradient at the point is 0.15 s⁻¹. What will be its viscosity (in Poise)?
A
2
B
0.5
C
0.2
D
20
Answer
The viscosity is 2 Poise.
Explanation
Solution
The relationship between shear stress (τ), dynamic viscosity (μ), and velocity gradient (dydu) is given by Newton's Law of Viscosity:
τ=μdydu
Given values:
- Shear stress (τ) = 0.03 N/m²
- Velocity gradient (dydu) = 0.15 s⁻¹
Calculate dynamic viscosity (μ) in SI units:
Rearrange the formula: μ=dyduτ
Substitute the values:
μ=0.15s−10.03N/m2=0.2N s/m2Convert viscosity to Poise:
1 Poise = 0.1 N s/m²
μ(in Poise)=0.2N s/m2×0.1N s/m21Poise=2Poise