Question
Question: $\sqrt{x} + \sqrt{y} \Rightarrow \sqrt{xy}$ $\frac{dy}{dx} \Rightarrow ?$...
x+y⇒xy dxdy⇒?
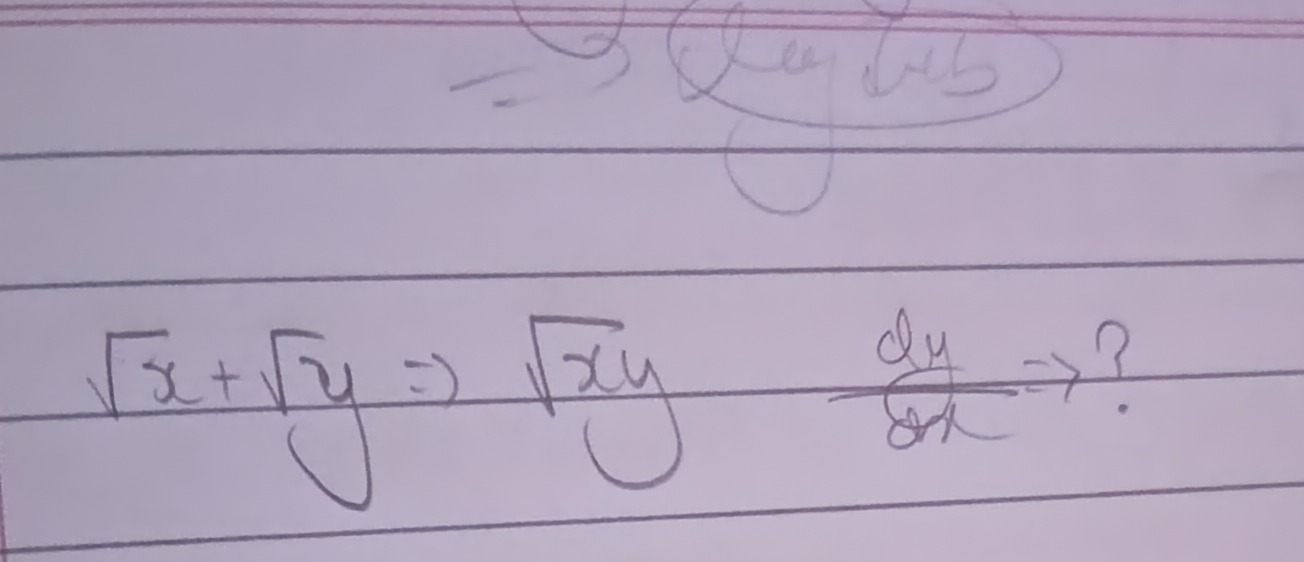
Answer
dxdy=−(x−1)31
Explanation
Solution
-
Rewrite x+y=xy using u=x and v=y to get (u−1)(v−1)=1.
-
Differentiate x+y=xy implicitly to obtain:
2x1+2y1dxdy=2xy1(y+xdxdy). -
Simplify and collect dxdy terms to get a relation.
-
Using the relation from the factorization, find the explicit derivative:
dxdy=−(x−1)31.
