Question

$\sqrt{\log_2(\frac{5x-x^2}{4})}$

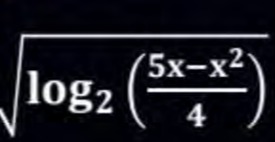
• A. The expression is defined for $0 < x < 5$.
• B. The expression is defined for $1 \le x \le 4$.
• C. The expression is defined for $x \le 1$ or $x \ge 4$.
• D. The expression is defined for all real numbers.

Answer 1

Answer: (B)

The domain for which the expression $\sqrt{\log_2(\frac{5x-x^2}{4})}$ is defined is $1 \le x \le 4$.

Answer 2

For the expression $\sqrt{\log_2(\frac{5x-x^2}{4})}$ to be defined in real numbers, two conditions must be met:

1. The argument of the logarithm must be strictly positive: $\frac{5x-x^2}{4} > 0$ $5x-x^2 > 0$ $x(5-x) > 0$ This inequality holds for $0 < x < 5$.

2. The argument of the square root must be non-negative: $\log_2\left(\frac{5x-x^2}{4}\right) \ge 0$ Since the base of the logarithm is $2 > 1$, we can exponentiate both sides: $\frac{5x-x^2}{4} \ge 2^0$ $\frac{5x-x^2}{4} \ge 1$ $5x-x^2 \ge 4$ $x^2 - 5x + 4 \le 0$ Factoring the quadratic $x^2 - 5x + 4 = 0$ gives $(x-1)(x-4) = 0$, so the roots are $x=1$ and $x=4$. Since the parabola opens upwards, the inequality $x^2 - 5x + 4 \le 0$ holds for $1 \le x \le 4$.

The domain of the expression is the intersection of the two conditions: $(0, 5) \cap [1, 4] = [1, 4]$.