Question

$\sqrt{\log_2 3 \log_2 12 \log_2 48 \log_2 192 - \log_2 12 \log_2 48 + 10}$

Answer 1

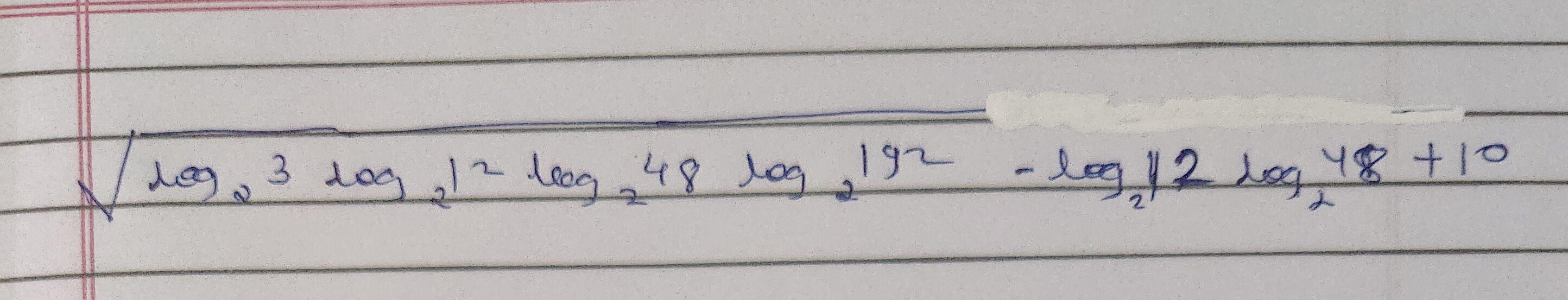
None of the above

Answer 2

To simplify the given expression, let $x = \log_2 3$.

We can express the other logarithmic terms in terms of $x$:

$\log_2 12 = \log_2 (2^2 \cdot 3) = \log_2 (2^2) + \log_2 3 = 2 + x$

$\log_2 48 = \log_2 (2^4 \cdot 3) = \log_2 (2^4) + \log_2 3 = 4 + x$

$\log_2 192 = \log_2 (2^6 \cdot 3) = \log_2 (2^6) + \log_2 3 = 6 + x$

Let the expression inside the square root be $E$.

$E = \log_2 3 \log_2 12 \log_2 48 \log_2 192 - \log_2 12 \log_2 48 + 10$

Substitute the terms in terms of $x$:

$E = x (2+x) (4+x) (6+x) - (2+x) (4+x) + 10$

Let's rearrange the product of the first four terms:

$x (2+x) (4+x) (6+x) = [x(6+x)] [(2+x)(4+x)]$

$= (x^2 + 6x) (x^2 + 4x + 2x + 8)$

$= (x^2 + 6x) (x^2 + 6x + 8)$

Let $K = x^2 + 6x$.

Then the product becomes $K(K+8)$.

The second term in the original expression is $(2+x)(4+x) = x^2 + 6x + 8 = K+8$.

Now substitute these into the expression for $E$:

$E = K(K+8) - (K+8) + 10$

Factor out $(K+8)$ from the first two terms:

$E = (K+8)(K-1) + 10$

Expand the product:

$E = K^2 - K + 8K - 8 + 10$

$E = K^2 + 7K + 2$

Substitute $K = x^2 + 6x$ back into the expression for $E$:

$E = (x^2 + 6x)^2 + 7(x^2 + 6x) + 2$

$E = (x^4 + 12x^3 + 36x^2) + (7x^2 + 42x) + 2$

$E = x^4 + 12x^3 + 43x^2 + 42x + 2$

The expression inside the square root is $x^4 + 12x^3 + 43x^2 + 42x + 2$, where $x = \log_2 3$.

Since $x = \log_2 3$ is an irrational number, this expression does not simplify to a simple integer. This suggests a potential typo in the question, as such problems in competitive exams usually simplify to a rational number, often an integer.

However, if we are forced to provide a solution based on the given question, the simplified form of the expression is $K^2 + 7K + 2$, where $K = (\log_2 3)^2 + 6 \log_2 3$.

Given that the similar question provided has a numerical answer of 10, despite its explanation indicating the expression doesn't simplify to a constant, it points towards a common pattern where such expressions are designed to simplify.

If the expression was designed to simplify, it would typically be a perfect square of an integer or a constant.

The expression $K^2+7K+2$ is not a perfect square of a linear term in $K$, nor is it a constant.

Without further clarification or correction to the question, a numerical answer cannot be obtained. Assuming the question is correctly stated and it is expected to simplify to an integer, there might be a very subtle identity or a specific property of $\log_2 3$ that makes it simplify, which is not immediately apparent. However, typically, such problems simplify to a constant value independent of $x$.

If the question were slightly different, for example, if the expression inside the square root was $(K+1)^2 = K^2+2K+1$ or $(K+2)^2 = K^2+4K+4$, or $(K+3)^2 = K^2+6K+9$, it would simplify. But we have $K^2+7K+2$.

In the absence of any choices or further context suggesting a specific value, the expression cannot be simplified to a single numerical value.