Question

If the ionization energy of $He^+$ is $19.6 \times 10^{-18}$ J per atom then the energy of $Be^{3+}$ ion in the second stationary state is :

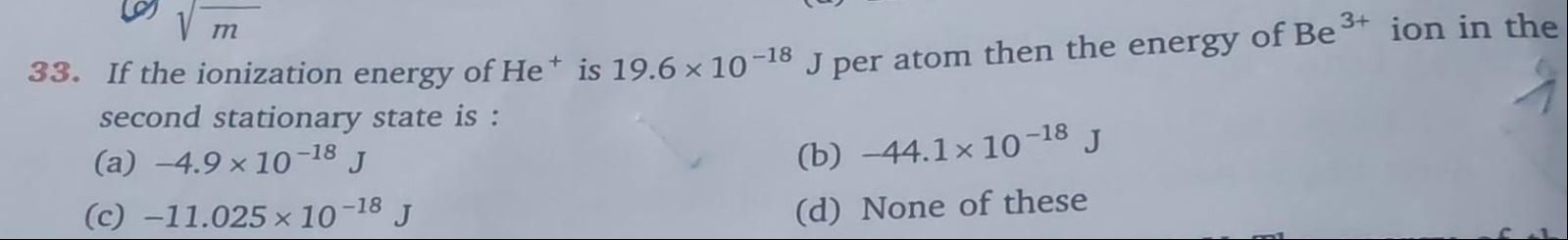
• A. -4.9 x 10^{-18} J
• B. -44.1 x 10^{-18} J
• C. -11.025 x 10^{-18} J
• D. None of these

Answer 1

Answer: (D)

None of these

Answer 2

The energy of an electron in the $n$-th stationary state of a hydrogen-like atom with atomic number $Z$ is given by the formula: $E_n = -k \frac{Z^2}{n^2}$ where $k$ is a constant. The ionization energy ($IE$) is the energy required to remove an electron from the ground state ($n=1$) to infinity ($n=\infty$), so $IE = E_{\infty} - E_1 = 0 - E_1 = -E_1$.

Given the ionization energy of $He^+$ ($Z=2$) is $19.6 \times 10^{-18}$ J. This means the energy of $He^+$ in its ground state ($n=1$) is $E_1(He^+) = -19.6 \times 10^{-18}$ J.

Using the formula for $He^+$ in the ground state ($Z=2, n=1$): $E_1(He^+) = -k \frac{2^2}{1^2} = -4k$

Equating this to the given ionization energy: $-19.6 \times 10^{-18} \text{ J} = -4k$ $k = \frac{19.6 \times 10^{-18}}{4} \text{ J} = 4.9 \times 10^{-18} \text{ J}$

Now, we need to find the energy of $Be^{3+}$ ($Z=4$) in the second stationary state ($n=2$). Using the same formula with the calculated constant $k$: $E_2(Be^{3+}) = -k \frac{Z_{Be}^2}{n^2}$ $E_2(Be^{3+}) = -(4.9 \times 10^{-18} \text{ J}) \frac{4^2}{2^2}$ $E_2(Be^{3+}) = -(4.9 \times 10^{-18} \text{ J}) \frac{16}{4}$ $E_2(Be^{3+}) = -(4.9 \times 10^{-18} \text{ J}) \times 4$ $E_2(Be^{3+}) = -19.6 \times 10^{-18} \text{ J}$

The calculated energy, $-19.6 \times 10^{-18}$ J, is not present in options (a), (b), or (c). Therefore, the correct option is (d).

The expression $\sqrt{\frac{V}{m}}$ at the beginning of the question is irrelevant to the problem.