Question
Question: $\sqrt{1 + \sin \theta}$ is equal to...
1+sinθ is equal to
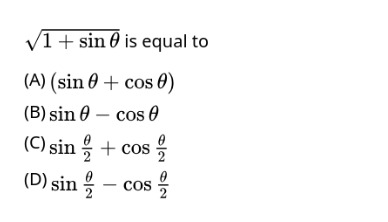
sinθ+cosθ
sinθ−cosθ
sin2θ+cos2θ
sin2θ−cos2θ
sin2θ+cos2θ
Solution
To simplify the expression 1+sinθ, we use fundamental trigonometric identities.
We know that:
- The Pythagorean identity: sin2x+cos2x=1.
- The double angle identity for sine: sin2x=2sinxcosx.
Let's apply these identities by setting x=2θ.
Then, we can write 1 as sin22θ+cos22θ, and we can write sinθ as 2sin2θcos2θ.
Substitute these into the expression 1+sinθ:
1+sinθ=(sin22θ+cos22θ)+(2sin2θcos2θ)
This expression is in the form of (a2+b2+2ab), which is the expansion of (a+b)2.
Here, a=sin2θ and b=cos2θ.
So, 1+sinθ=(sin2θ+cos2θ)2.
Now, we need to find the square root of this expression:
1+sinθ=(sin2θ+cos2θ)2
Therefore, 1+sinθ=sin2θ+cos2θ.
Given the options, the most appropriate answer is the simplified form without the absolute value, assuming the principal root and a suitable domain for θ.
