Question

Speed of point P is:

$\text{A}. \ 4\sqrt{2} ms^{-1}$
$\text{B}. \ 2\sqrt{5} ms^{-1}$
$\text{C}. \ \sqrt{5} ms^{-1}$
$\text{D}. \ 5 ms^{-1}$

Answer 1

Speed is a scalar quantity. Speed means the magnitude of net velocity. Velocity is a vector quantity. Hence for a body or point, the net velocity is the vector sum of all the velocities in different directions. Coming to rotational + translational motion. If a body undergoes both rotational and translational motion, then every point of the body will have two kinds of velocities, one due to translational motion and other due to rotational motion.

Formula used:
$\vec{v_{r}} = \vec{\omega} \times \vec{R}$, $\vec{v_{net}}= \vec{v_{r}}+\vec{v_{t}}$
Where $\vec{v_{r}}$ is the velocity due to rotation and $\vec\omega$ is the angular velocity of the wheel.

Complete step-by-step answer:
For translational motion of the wheel, the transitional velocity of all the points lying on the wheel is the same and is equal to the velocity of the centre of mass. Hence transitional velocity ($\vec{v_{t}}$) of point P is $4ms^{-1}$ in positive x direction. Now using $\vec{v_{r}} = \vec{\omega} \times \vec{R}$, For constant angular velocity, we can write $v_{r}=\omega R$, with direction as tangent to the circle at that point. But here, R is not given.
To find R, we will apply no slip condition of the contact point O. Means in case of no slipping, velocity of point of contact with ground is zero.

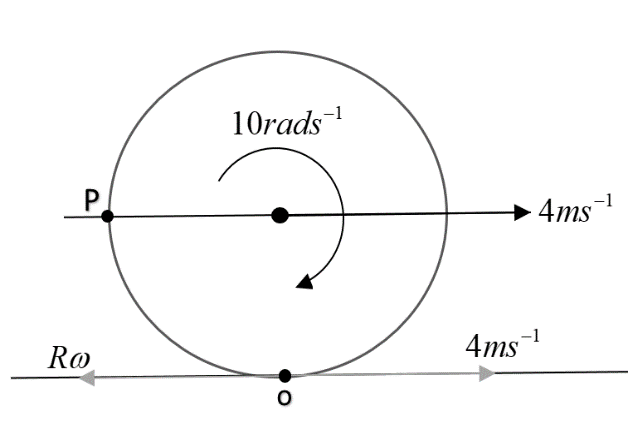
As shown in figure, O has two velocities in opposite directions. To cancel out the velocity, these velocities must be equal. Hence $R\omega$ = 4.
Now, for point P;

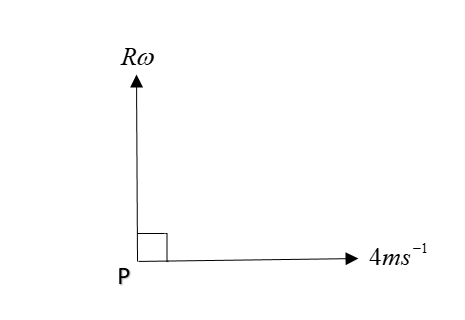
Point P will have two velocity in perpendicular direction, hence we will add them by vector addition:
$\vec{v_{net}}= \vec{v_{r}}+\vec{v_{t}}$
Or $|\vec{v_{net}}|= \sqrt{{\vec{v_{r}}^2}+{\vec{v_{t}}^2}+2v_{r}v_{t}cos \ 90^{\circ}}$
Or $|\vec{v_{net}}|= \sqrt{{{(R \omega)}^2}+{4}^2 }$ [ $cos \ 90^\circ = 0$]
Or $|v_{net}|= \sqrt{4^2+4^2}$= $4 \sqrt2 ms^{-1}$ [ $R\omega$ = 4 ]
Hence speed, which is magnitude of velocity is $4 \sqrt2 ms^{-1}$.
So, the correct answer is “Option A”.

Note: In these types of questions, students should give emphasis on slipping conditions. If there is not a pure rolling condition, then even the contact point does not have velocity zero. But in general, if there’s a pure rolling, then one must remember that the velocity of the contact point is zero whereas the velocity of the uppermost point is 2 times the velocity of the centre of mass.