Question
Question: Special cases (a) If, e = 1 (perfectly elastic collision) (b) e = 0 (perfectly inelastic collision)...
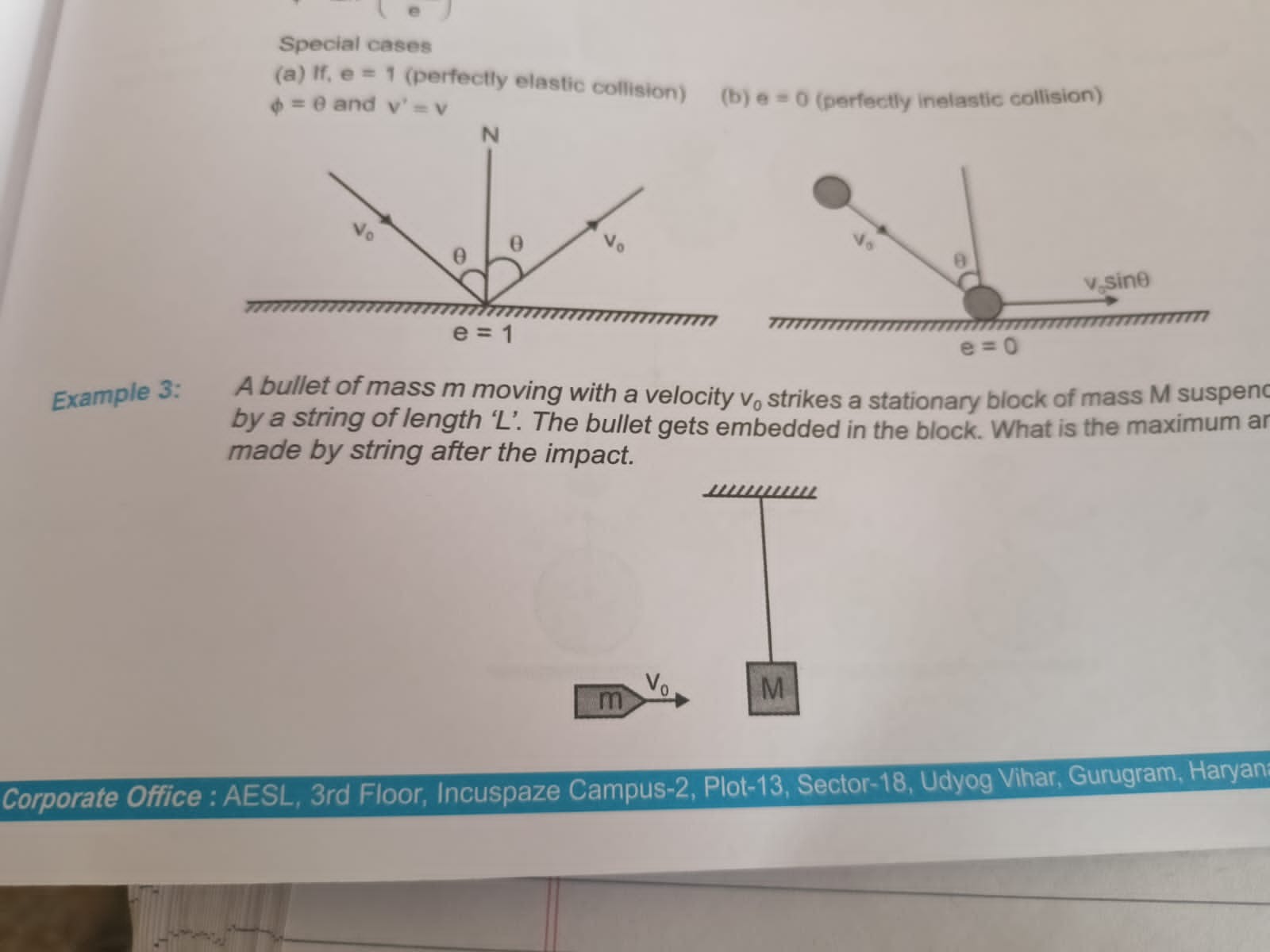
Special cases
(a) If, e = 1 (perfectly elastic collision) (b) e = 0 (perfectly inelastic collision) ϕ=θ and v' = v
Example 3: A bullet of mass m moving with a velocity v0 strikes a stationary block of mass M suspenc by a string of length 'L'. The bullet gets embedded in the block. What is the maximum ar made by string after the impact.
θ=arccos[1−2gL(m+M)2m2v02]
Solution
The problem involves two distinct phases:
- A perfectly inelastic collision: The bullet strikes the block and gets embedded. During this collision, linear momentum is conserved, but mechanical energy is not.
- Pendulum motion: After the collision, the combined bullet-block system swings upwards like a simple pendulum. During this phase, mechanical energy is conserved.
Phase 1: Perfectly Inelastic Collision
Let V be the velocity of the combined bullet-block system immediately after the impact.
Before collision:
- Mass of bullet =
m, velocity =v₀ - Mass of block =
M, velocity =0(stationary)
After collision:
- Combined mass =
(m + M), velocity =V
Applying the principle of conservation of linear momentum:
Initial momentum = Final momentum
m * v₀ + M * 0 = (m + M) * V
m * v₀ = (m + M) * V
Solving for V, the velocity of the combined system just after impact:
V=m+Mmv0
Phase 2: Pendulum Motion
The combined mass (m + M) starts with velocity V at the lowest point (its initial height can be considered h₁ = 0). It swings upwards to a maximum height h where its velocity momentarily becomes 0.
Applying the principle of conservation of mechanical energy between the lowest point (immediately after collision) and the highest point of the swing:
Initial Kinetic Energy + Initial Potential Energy = Final Kinetic Energy + Final Potential Energy 21(m+M)V2+(m+M)g(0)=21(m+M)(0)2+(m+M)gh 21(m+M)V2=(m+M)gh h=2gV2
Now, we need to relate this maximum height h to the maximum angle θ made by the string with the vertical.
From the geometry of a simple pendulum of length L swinging to a maximum angle θ, the vertical height h risen from the lowest point is given by:
h=L−Lcosθ
h=L(1−cosθ)
Equating the two expressions for h:
L(1−cosθ)=2gV2
1−cosθ=2gLV2
cosθ=1−2gLV2
Substitute the expression for V from Phase 1 into this equation:
V2=(m+Mmv0)2=(m+M)2m2v02
So,
cosθ=1−2gL(m+M)2m2v02
Finally, the maximum angle θ is:
θ=arccos[1−2gL(m+M)2m2v02]
The maximum angle made by the string after the impact is given by the above formula.
Explanation of the solution:
- Conservation of Linear Momentum: Apply to the perfectly inelastic collision of the bullet and block to find their combined velocity
Vimmediately after impact. - Conservation of Mechanical Energy: Apply to the subsequent pendulum motion. The kinetic energy of the combined mass at the lowest point is converted into potential energy at the maximum height
h. - Geometry: Relate the maximum height
hto the string lengthLand the maximum angleθusing pendulum geometry (h = L(1 - cosθ)). - Substitution: Substitute the expression for
Vinto the energy conservation equation, then solve forθ.
